The pressure-volume work for an ideal gas can be calculated by using the expression W=−∫VfViPexdV. The work can also be calculated from the pV - plot by using the area under the curve within the specified limits. When an ideal gas is compressed (i) reversibly or (ii) irreversibly from volume Vi to Vf. Choose the correct option.
Wreversible=Wirreversible
Wreversible<Wirreversible
Wreversible>Wirreversible
Wreversible=Wirreversible+PexΔV
The correct Answer is:B
To solve the problem regarding the work done on an ideal gas during reversible and irreversible compression, we can follow these steps:
Step 1: Understand the Work Done Expression
The work done on an ideal gas during compression can be expressed mathematically as:
W=−∫VfViPexdV
Where:
- W is the work done,
- Vi is the initial volume,
- Vf is the final volume,
- Pex is the external pressure.
Step 2: Analyze the PV Diagram
Draw a Pressure-Volume (PV) diagram for both reversible and irreversible compression.
- For reversible compression, the process is carried out slowly, allowing the system to remain in equilibrium. The curve will be smooth and continuous.
- For irreversible compression, the process occurs rapidly, and the path taken will be different, typically resulting in a steeper curve.
Step 3: Identify the Areas Under the Curves
In the PV diagram:
- The area under the curve for reversible compression represents the work done Wreversible.
- The area under the curve for irreversible compression represents the work done Wirreversible.
Step 4: Compare the Work Done
Since both processes start at the same initial volume Vi and end at the same final volume Vf:
- The area under the curve for irreversible compression is generally larger than that for reversible compression due to the higher external pressure acting over a larger volume change.
- Thus, we can conclude that:
Wirreversible>Wreversible
Step 5: Choose the Correct Option
Based on the analysis, the correct option is:
- W irreversible is more than W reversible.
Final Answer
The correct option is W irreversible > W reversible.
---
The work done on an ideal gas during compression can be expressed mathematically as:
W=−∫VfViPexdV
Where:
- W is the work done,
- Vi is the initial volume,
- Vf is the final volume,
- Pex is the external pressure.
Draw a Pressure-Volume (PV) diagram for both reversible and irreversible compression.
- For reversible compression, the process is carried out slowly, allowing the system to remain in equilibrium. The curve will be smooth and continuous.
- For irreversible compression, the process occurs rapidly, and the path taken will be different, typically resulting in a steeper curve.
In the PV diagram:
- The area under the curve for reversible compression represents the work done Wreversible.
- The area under the curve for irreversible compression represents the work done Wirreversible.
Since both processes start at the same initial volume Vi and end at the same final volume Vf:
- The area under the curve for irreversible compression is generally larger than that for reversible compression due to the higher external pressure acting over a larger volume change.
- Thus, we can conclude that:
Wirreversible>Wreversible
Based on the analysis, the correct option is:
- W irreversible is more than W reversible.
The correct option is W irreversible > W reversible.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSERTION & REASON15videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Thermodynamic Terms3videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HIGHER ORDER THINKING SKILLS8videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THE S-BLOCK ELEMENTSEXERCISE - Assertion And Reason15videos
THE S-BLOCK ELEMENTS
Similar Questions
The pressure volume work for an ideal gas can be calculated by using the expression w=−∫vfViPexdV. The work can also be calculated from the pV-plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (B) irreversibly from volume Vi to Vf choose the correct option.
View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionFor an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using expression =−nRTln.VfVi. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversible to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option
View SolutionThe pressure and volume of an ideal gas are related as pα1v2 for process A→B as shown in figure . The pressure and volume at A are 3p0andv0 respectively and pressure B is p0 the work done in the process A→B is found to be [x−√3]p0v0 find
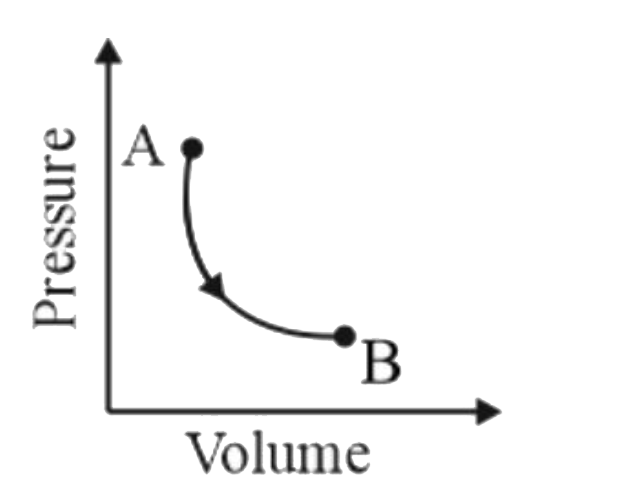 View Solution
View SolutionGraphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from (pi,Vi) to (pf,Vf). With the help of a pV plot compare the work done in the above case with that carried out against a constant pressure pf.
View SolutionA gas is expanded from volume V1 to V2 through three different process:
a. Reversible adiabatic
b. Reversible isothermal
c. Irreversible adiabatic (against a constant external pressure Pex)
The correct option isView SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
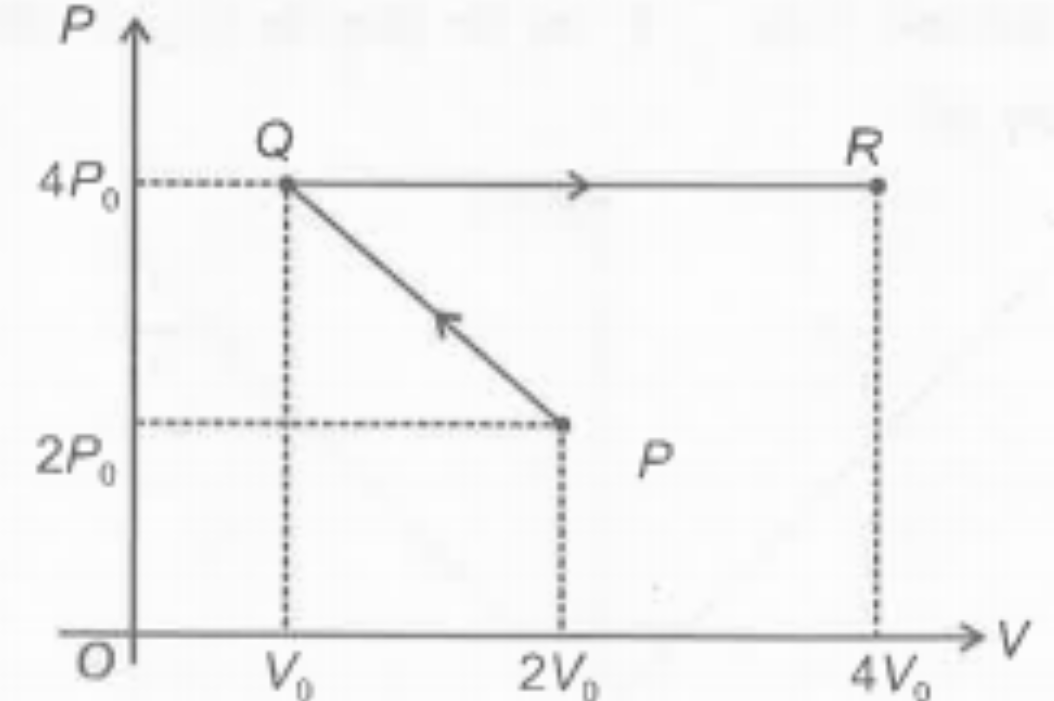 View Solution
View SolutionWhich of the following volume-temperature (V−I) plots represents the behaviour of 1mole of an ideal gas at the atmospheric pressure?
View SolutionAn ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
View SolutionA gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
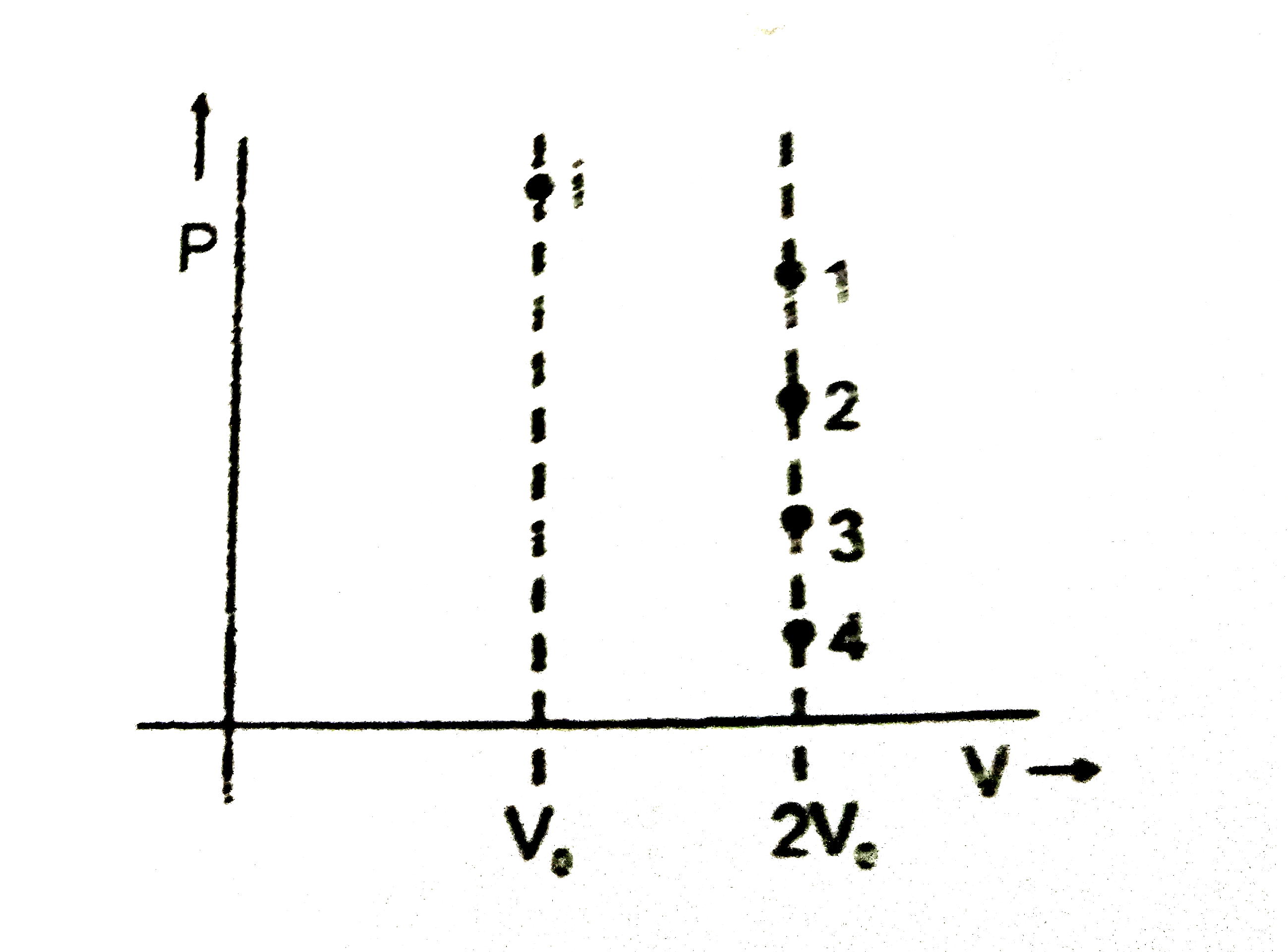 View Solution
View Solution

