The radioactive series whose end product is .20983Bi is
Thorium series
Fourier series
Actinium series
Neptunium series
The correct Answer is:D
To determine the radioactive series whose end product is 20983Bi (Bismuth-209), we need to analyze the possible radioactive series and their starting isotopes.
1. Identify the Options: We have four radioactive series to consider:
- Thorium series
- Uranium series (specifically, the Actinium series)
- Neptunium series
2. Thorium Series:
- The thorium series starts from 23290Th (Thorium-232).
- To reach Bismuth-209, we calculate the mass decay:
232−209=23
- This means we would need to decay 23 mass units. This is not feasible through a series of alpha and beta decays.
3. Actinium Series:
- The actinium series starts from 23592U (Uranium-235).
- To reach Bismuth-209, we calculate the mass decay:
235−209=26
- This would require 6.5 alpha particles, which is not practically possible since we cannot have half a particle.
4. Neptunium Series:
- The neptunium series starts from 23793Np (Neptunium-237).
- To reach Bismuth-209, we calculate the mass decay:
237−209=28
- This decay is feasible as it can occur through a series of alpha and beta decays.
5. Conclusion:
- The radioactive series whose end product is 20983Bi is the Neptunium series.
Final Answer:
The radioactive series whose end product is 20983Bi is the Neptunium series.
- Thorium series
- Uranium series (specifically, the Actinium series)
- Neptunium series
- The thorium series starts from 23290Th (Thorium-232).
- To reach Bismuth-209, we calculate the mass decay:
232−209=23
- This means we would need to decay 23 mass units. This is not feasible through a series of alpha and beta decays.
- The actinium series starts from 23592U (Uranium-235).
- To reach Bismuth-209, we calculate the mass decay:
235−209=26
- This would require 6.5 alpha particles, which is not practically possible since we cannot have half a particle.
- The neptunium series starts from 23793Np (Neptunium-237).
- To reach Bismuth-209, we calculate the mass decay:
237−209=28
- This decay is feasible as it can occur through a series of alpha and beta decays.
- The radioactive series whose end product is 20983Bi is the Neptunium series.
The radioactive series whose end product is 20983Bi is the Neptunium series.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - NUCLEAR CHEMISTRY EXERCISE - Ordinary Thinking (Rate of decay and Half - life)97videos
NUCLEAR CHEMISTRY
- BOOK - ERRORLESS CHAPTER - NUCLEAR CHEMISTRY EXERCISE - Ordinary Thinking (Artificial transmutation )59videos
NUCLEAR CHEMISTRY
- BOOK - ERRORLESS CHAPTER - NUCLEAR CHEMISTRY EXERCISE - JEE SECTION (Matrix Match Type Questions)2videos
NUCLEAR CHEMISTRY
- BOOK - ERRORLESS CHAPTER - NITROGEN CONTAINING COMPOUNDS EXERCISE - JEE (ADVANCED) 2018 MORE THAN ONE CHOICE CORRECT ANSWER1videos
NITROGEN CONTAINING COMPOUNDS
- BOOK - ERRORLESS CHAPTER - ORES, MINERALS AND METALLURGICAL EXTRACTIONEXERCISE - JEE ANSWER TPYE QUESTION (JEE Advanced) 2018) Numeric answer type question1videos
ORES, MINERALS AND METALLURGICAL EXTRACTION
Similar Questions
Knowledge Check
- Question 1 - Select One
End product will be.
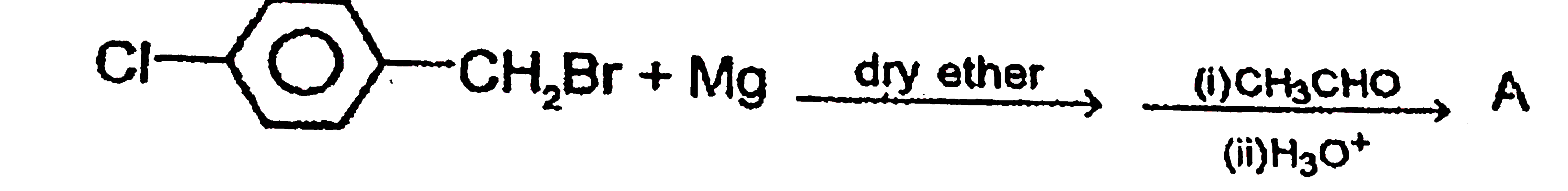 A
A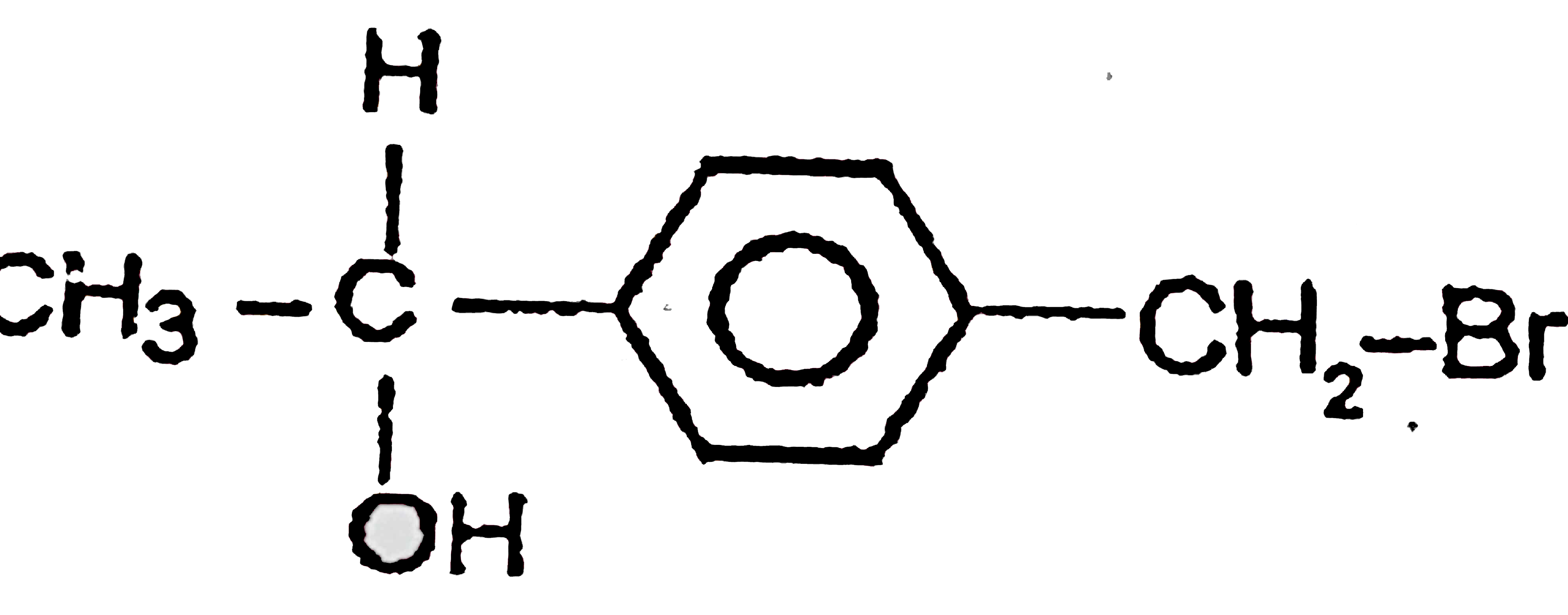 B
B C
C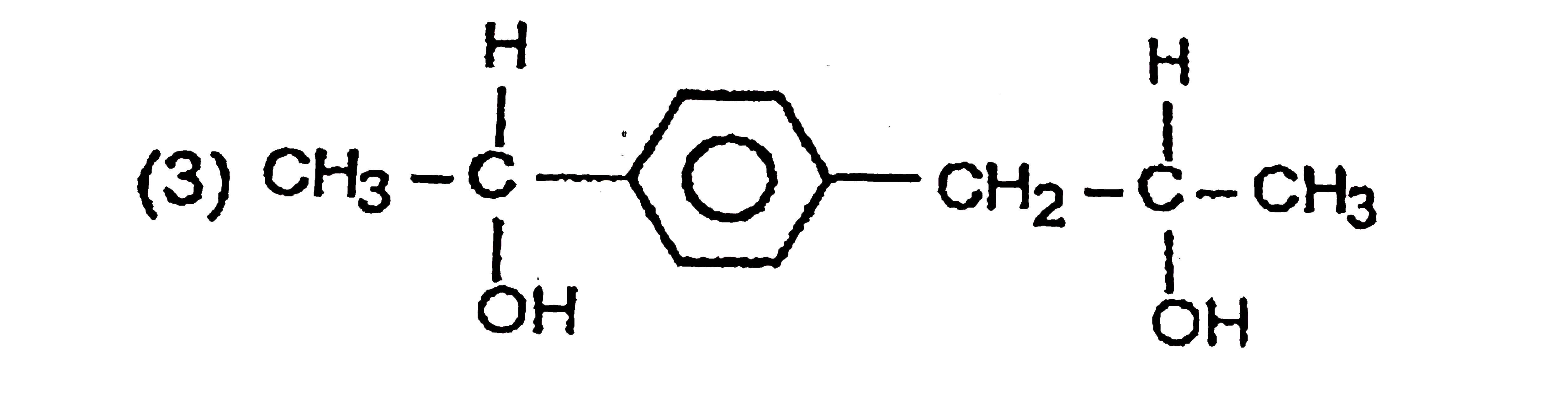 D
D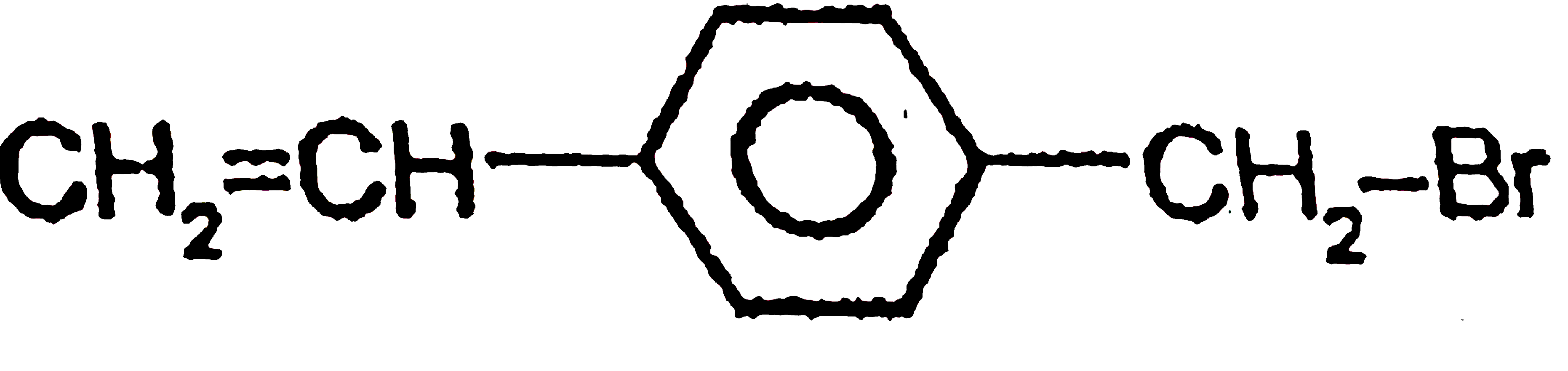
- Question 2 - Select One
Which radioactive series do not show emanation?
ATh− seriesBNp− seriesCU− seriesDAc− series - Question 3 - Select One
The end product of (4n+3) series if ?
A.83Bi209B.82Pb207C.83Pb206D.83Bi208
Thorium .29890Bi The produces a daughter nucleus that is radioactive. The augther in turn, produces it own radioactive daugher and so on. This process continues until bismuth .21283Bi is reaches. What are the total number Nα of α-particle and the total number Nβ of β−-paricles that are generated in this series or radioactive decays?
View SolutionOne of naturally occurring radioactive decay series begins with _(90)232Th and ends with a stable _(82)208Pb.
How many beta (β) decays are there in this series? Show by calculate.View SolutionA radioactive element X emits six α-particles and four β-particles leading to end product 20882Pb. X is
View SolutionThe end product of 4n series is
View SolutionThe end product of 4n series is a).82Pb208 b).82Pb207 c).82Pb209 d).82Pb204
View Solution

