The rate constant for the first order decomposition of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life period be 256min?
Arrhenius equation is given by ,
k=Ae−Ea/RT
⇒ ln k = ln A −EaRT
⇒ ln k = log A −EaRT
⇒ log k = log A −Ea2.303RT (i)
The given equation is
log k = 14.34−1.25×104K/T (ii)
From equation (i) and (ii) , we obtain
Ea2.303RT=1.25×104KT
⇒Ea=1.25×104K×2.303×R
=1.25×104K×2.303×8.314JK−1mol−1
= 239339.3Jmol−1 (approximately)
= 239.34kJmol−1
Also , when t1/2 = 256 minutes
k=0.693t12
= 0.693256
= 2.707×10−3min−1
=4.51×10−5s−1
It is also given that log k = 14.34−1.25×104K/T
⇒ log (4.51×10−5)=14.34−1.25×104KT
⇒log(0.654−05)=14.34−1.25×104KT
⇒1.25×104KT=18.686
⇒T=1.25×104K18.686
= 668. 85 K
= 669 K (approximately)
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - NCERTCHAPTER - CHEMICAL KINETICSEXERCISE - Exercise
1 Videos
- CHEMICAL KINETICSBOOK - NCERTCHAPTER - CHEMICAL KINETICSEXERCISE - SOLVED EXAMPLE
1 Videos
- BIOMOLECULESBOOK - NCERTCHAPTER - BIOMOLECULESEXERCISE - Exercise
33 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - NCERTCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Exercise
32 Videos
Similar Questions
The rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View Solution
Knowledge Check
The rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
Energy of activation (in kcal) isA57.6kcalB1.25×104kcalC14.0kcalD14×104kcalThe rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
Pre-exponential factor for this reaction isA14s−1B1014s−1C10−14s−1D1.25×104s−1The rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
At what temperature, rate constant is equal to pre-exponential factor?AT=1.25×104K14BT=∞CT=0D(14−1.25×104)K
Rate constant for the decomposition of ethylene oxide into CH4 and CO may be described by the equation logl(s−1)=14.34−1.25×104T
(a) What is the energy of activation of this reaction ?
(b) What is the value of k at 670K ?
View SolutionRate constant for the decomposition of ethylene oxide into CH4 and CO may be described be the equation. logk(s)−1=14.34−1.25×104T
(a) What is the energy of activation of this reaction ?
(b) What is the value of k at 670K ?
View SolutionThe rate constant of the first order reaction , that is decomposition of ethylene oxide into CH4 and CO, may be described by the following equation
logk(s−1)=14.34−1.25×104TK
Find (a) energy of activation ,
View SolutionThe rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
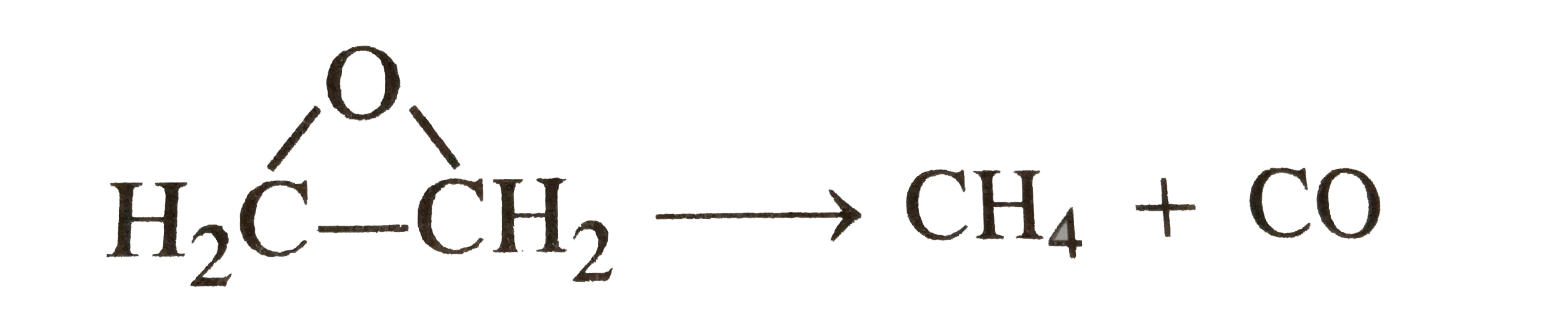
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction is
View SolutionThe rate constant for the decompoistion of a certain reaction is described by the equation:
logk(s−1)=14−1.25×104KT
What is the effect on the rate of reaction at 127∘C, if in the presence of catalyst, energy of activation is lowered by 10kJmol−1?
View Solution
