The slope in the plot of ln[R] vs. time gives
(where [R] is the final concentration of reactant.)
+k
+k2.303
−k
−k2.303
The correct Answer is:C
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) EXERCISE - SECTION -B
7 Videos
- CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) EXERCISE - SECTION -C
7 Videos
- CBSE EXAMINATION PAPER 2020 BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION D
6 Videos
- CHEMICAL KINETICS BOOK - U-LIKE SERIESCHAPTER - CHEMICAL KINETICS EXERCISE - SELF ASSESSMENT TEST (SECTION D)
1 Videos
Similar Questions
Knowledge Check
The slope in the plot of ln[R] vs. time gives in first order reaction
A+kB+k2.303C−kD−k2.303A plot of reactant concentration versus time for a reaction is a straight line with a negative slope giving the rate constant, and the intercept, giving the initial concentration of the reactant. The order of the reaction is
A0B1C2Dnone of theseFor a first order reaction, we obtain a straight line with positive slope, what we need to plot?
A−log10[A] vs tB−loge[A] vs tClog10[A]vs log tD[A] vs t
Plotting log10t1/2 against log10[A0] (where A0 is the initial concentration of a reactant) for a fist order reaction the slope will be
View SolutionWrite the slope value obtained in the plot of log [R0]/[R] vs time for a first order reaction.
View SolutionPlotting log10t1/2 against log10[A0] (where A0 is the initial concentration of a reactant) for a fist order reaction the slope will be
View SolutionFor a second order reaction, 2A→ Products, a plot of log t1/2 vs log a (where a is initial concentration) will give an intercept equal to which one of the following?
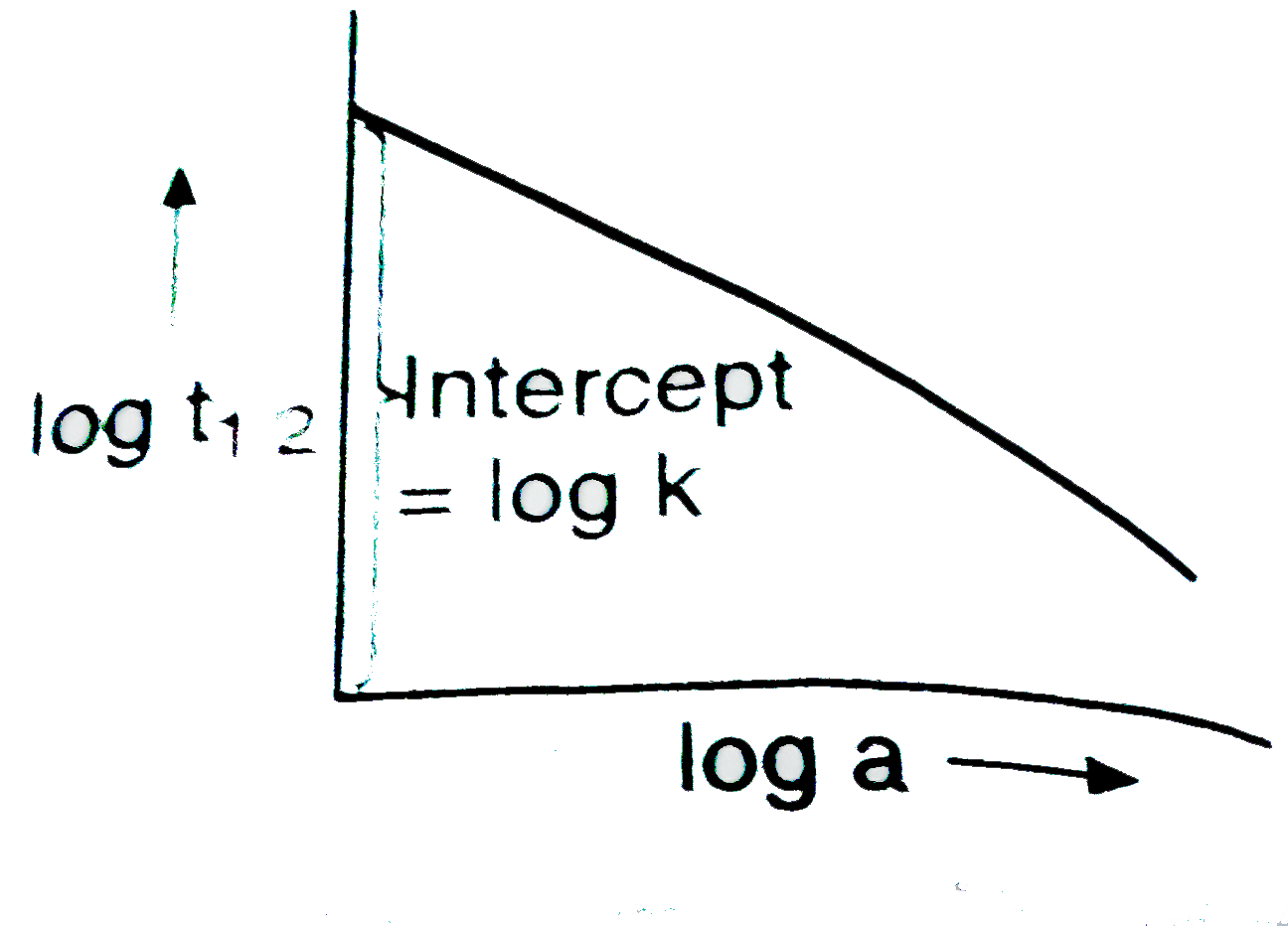
View SolutionFor a second order reaction, 2A→ Products, a plot of log t1/2 vs log a (where a is initial concentration) will give an intercept equal to which one of the following?

View Solution
