The smallest aldose which is able to form cyclic hemiacetal :
D-glyceraldehyde
D-Erythrose
D-Threose
D-Ribose
The correct Answer is:B, C
To determine the smallest aldose that can form a cyclic hemiacetal, we need to analyze the structures of the given aldoses and understand the requirements for hemiacetal formation.
1. Identify the Aldoses: The aldoses given in the question are:
- D-glyceraldehyde
- D-erythrose
- D-threose
- D-ribose
2. Draw the Structures:
- D-glyceraldehyde: This is a 3-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl).
- D-erythrose: This is a 4-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl).
- D-threose: This is also a 4-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl).
- D-ribose: This is a 5-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl, C5: hydroxyl).
3. Determine the Minimum Carbon Requirement:
- To form a cyclic hemiacetal, a minimum of 4 carbons is required. This is because the aldehyde group on the first carbon must react with a hydroxyl group on one of the other carbons to form a ring structure.
4. Analyze Each Aldose:
- D-glyceraldehyde: With only 3 carbons, it cannot form a cyclic hemiacetal.
- D-erythrose: With 4 carbons, it can form a cyclic hemiacetal.
- D-threose: With 4 carbons, it can also form a cyclic hemiacetal.
- D-ribose: Although it has 5 carbons, it is not the smallest aldose that can form a cyclic hemiacetal.
5. Conclusion: The smallest aldoses that can form cyclic hemiacetals are D-erythrose and D-threose.
Final Answer:
The smallest aldoses which can form cyclic hemiacetals are D-erythrose and D-threose.
- D-glyceraldehyde
- D-erythrose
- D-threose
- D-ribose
- D-glyceraldehyde: This is a 3-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl).
- D-erythrose: This is a 4-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl).
- D-threose: This is also a 4-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl).
- D-ribose: This is a 5-carbon aldose (C1: aldehyde, C2: hydroxyl, C3: hydroxyl, C4: hydroxyl, C5: hydroxyl).
- To form a cyclic hemiacetal, a minimum of 4 carbons is required. This is because the aldehyde group on the first carbon must react with a hydroxyl group on one of the other carbons to form a ring structure.
- D-glyceraldehyde: With only 3 carbons, it cannot form a cyclic hemiacetal.
- D-erythrose: With 4 carbons, it can form a cyclic hemiacetal.
- D-threose: With 4 carbons, it can also form a cyclic hemiacetal.
- D-ribose: Although it has 5 carbons, it is not the smallest aldose that can form a cyclic hemiacetal.
The smallest aldoses which can form cyclic hemiacetals are D-erythrose and D-threose.
Topper's Solved these Questions
- BIOMOLECULESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Exercises (Single Correcttype)
80 Videos
- BIOMOLECULESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Exercises (Assertion-Reasoning)
15 Videos
- BIOMOLECULESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Exercises (Linked Comprehension)
36 Videos
- AROMATIC COMPOUNDS AND ALKYL AND ARYL HALIDES BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - AROMATIC COMPOUNDS AND ALKYL AND ARYL HALIDES EXERCISE - Archives Subjective Type
4 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
Similar Questions
Knowledge Check
Which of following compound is hemiacetal ?
A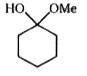 B
B C
C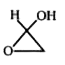 Dall of these
Dall of these
The smallest organisms which cause diseases among plants are
View SolutionAssertion: Glucose does not gives 2,4-DNP test.
Reason: Glucose exists in cyclic hemiacetal form
View SolutionThe smallest natural number of the form 123x43y, which is exactly divisible by 6 is
View SolutionThe smallest viable unit which can grow, multiply and form a plant in tissue culture is
View SolutionVersatile anthers which are able to swing freely are found in
View SolutionWhich is the smallest whole number?
View SolutionIn which of the following cyclic ring is a parent chain :
View Solution
