The variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
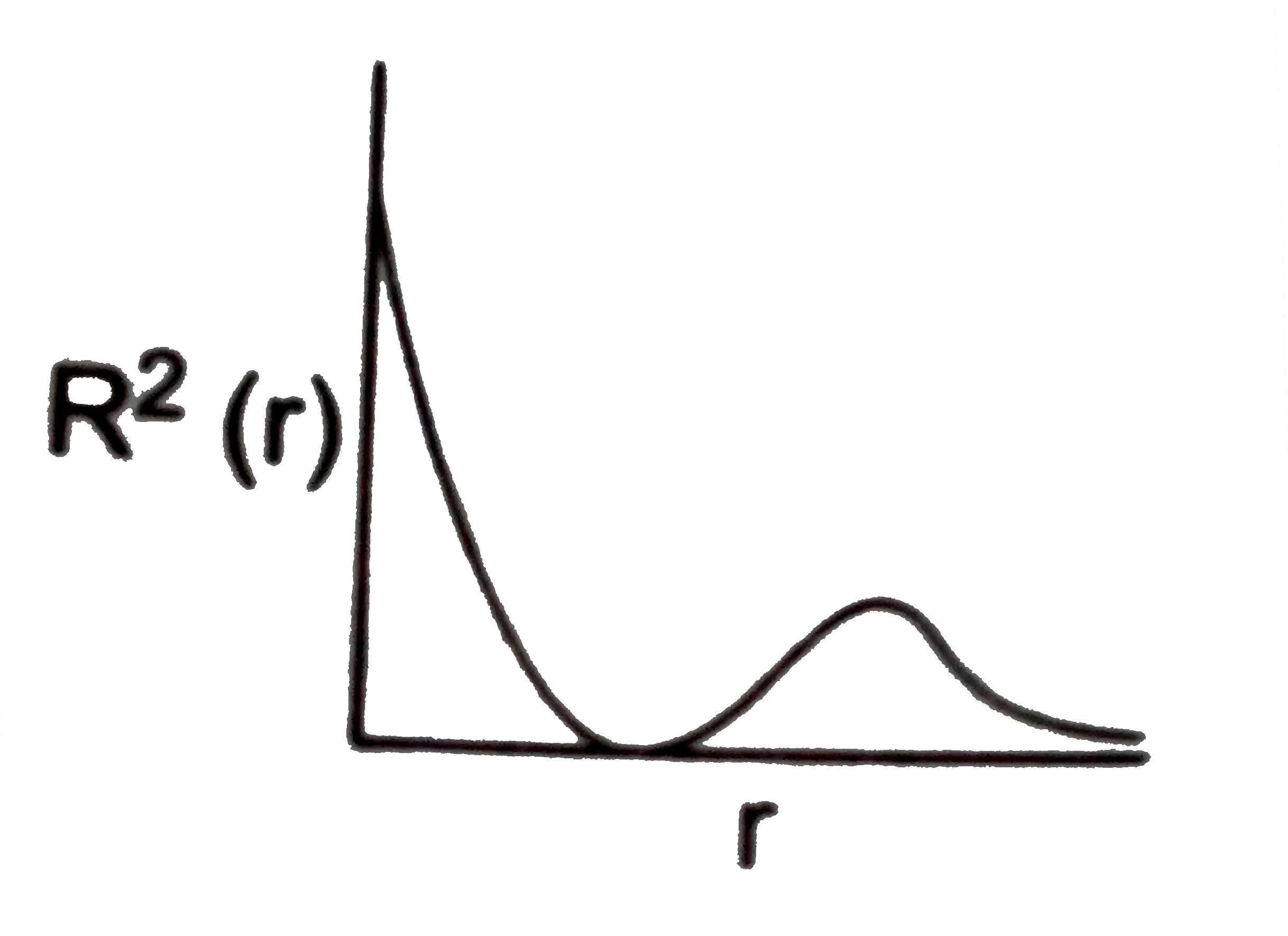
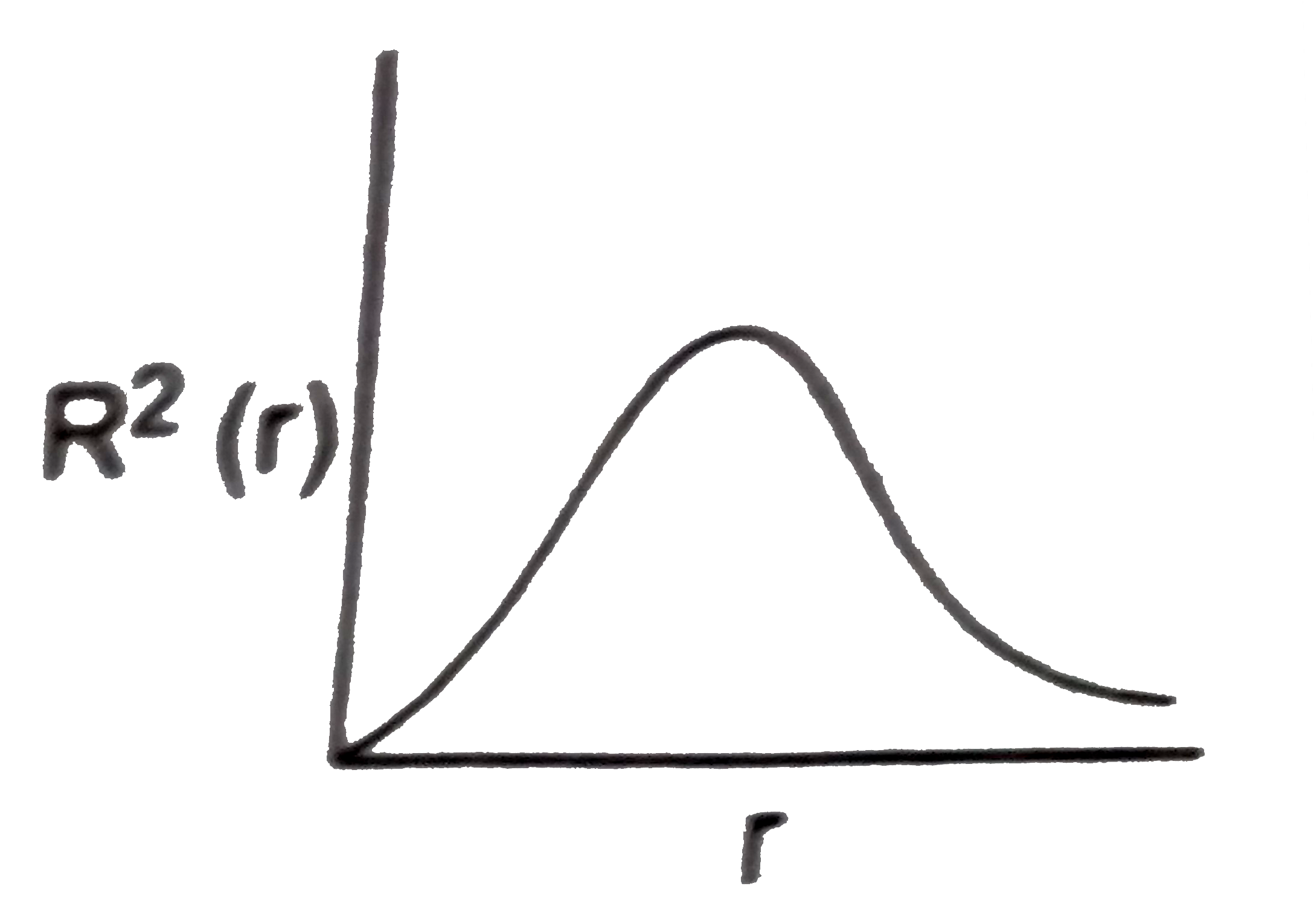
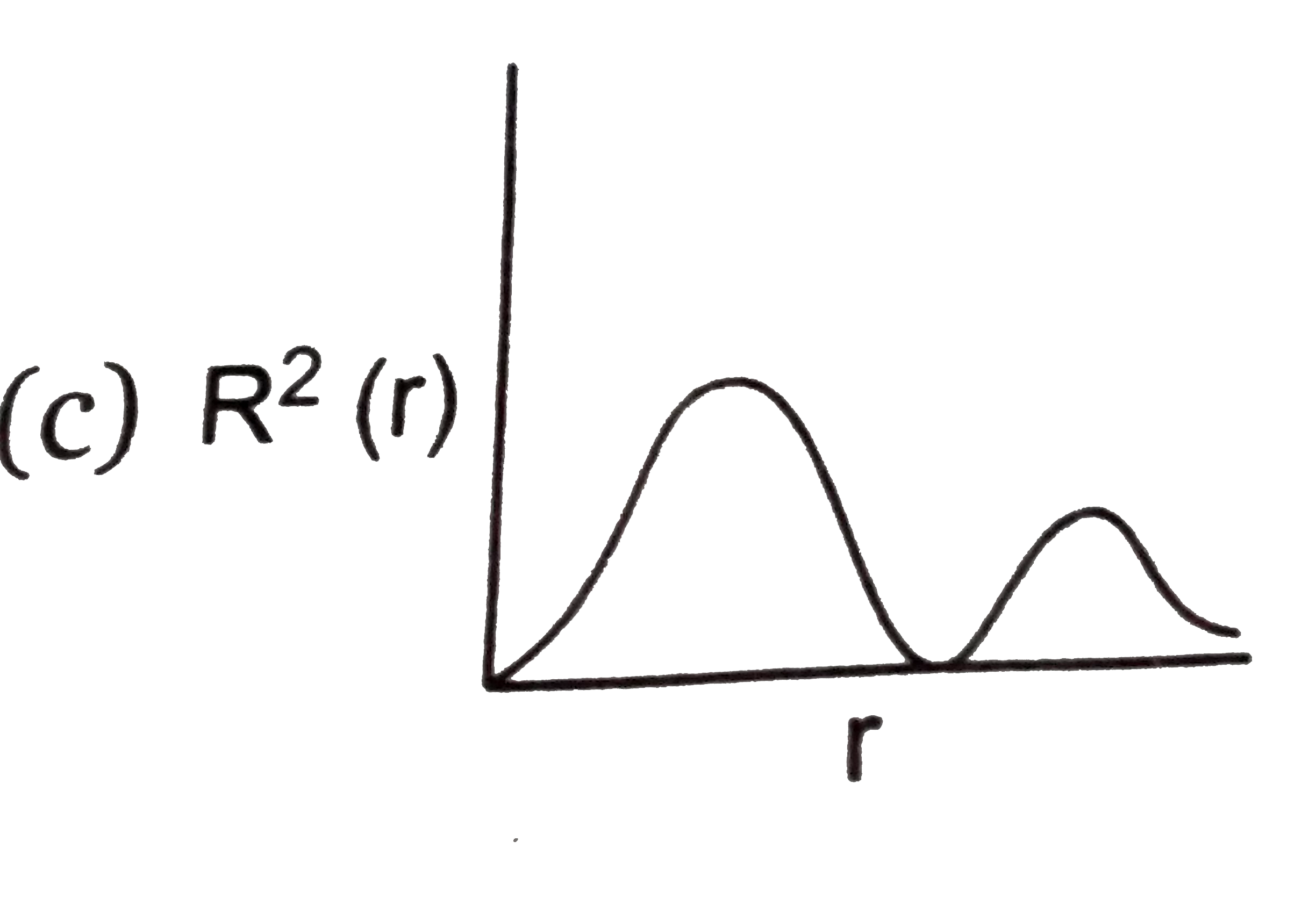
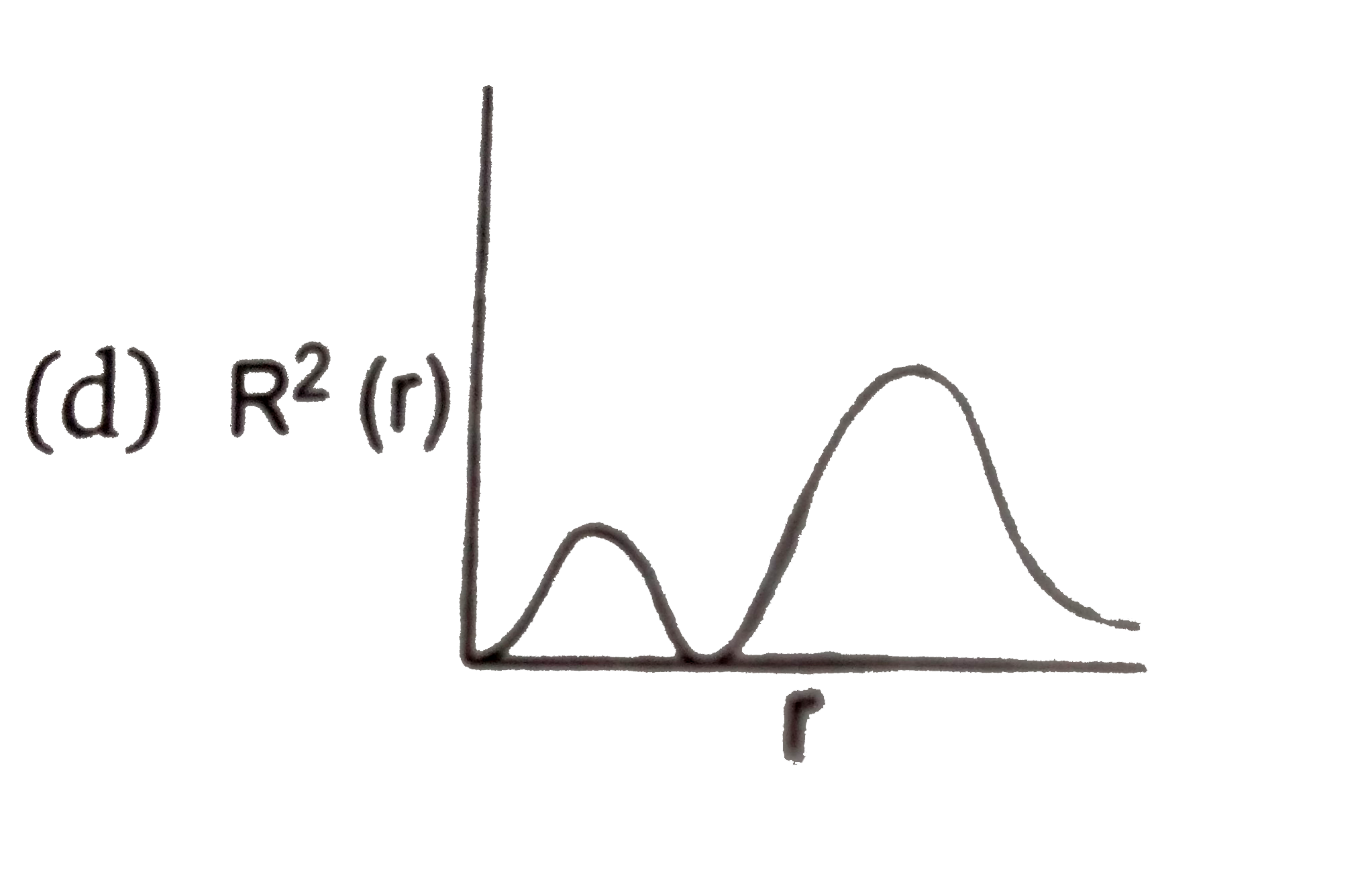
Step by step video & image solution for The variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Assertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical
Reason. Probability density is Ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.AIf both assertion and reason are true, and reason is the true explanation of the assertionBIf both assertion and reason are true, but reason is not the true explanation of the assertionCIf assertion is true, but reason is falseDIf both assertion and reason are falseWhich of the following is correct graph between Probability density sπ2(r) vs radial distance of electron (r) form nucleus for 3 s ?
A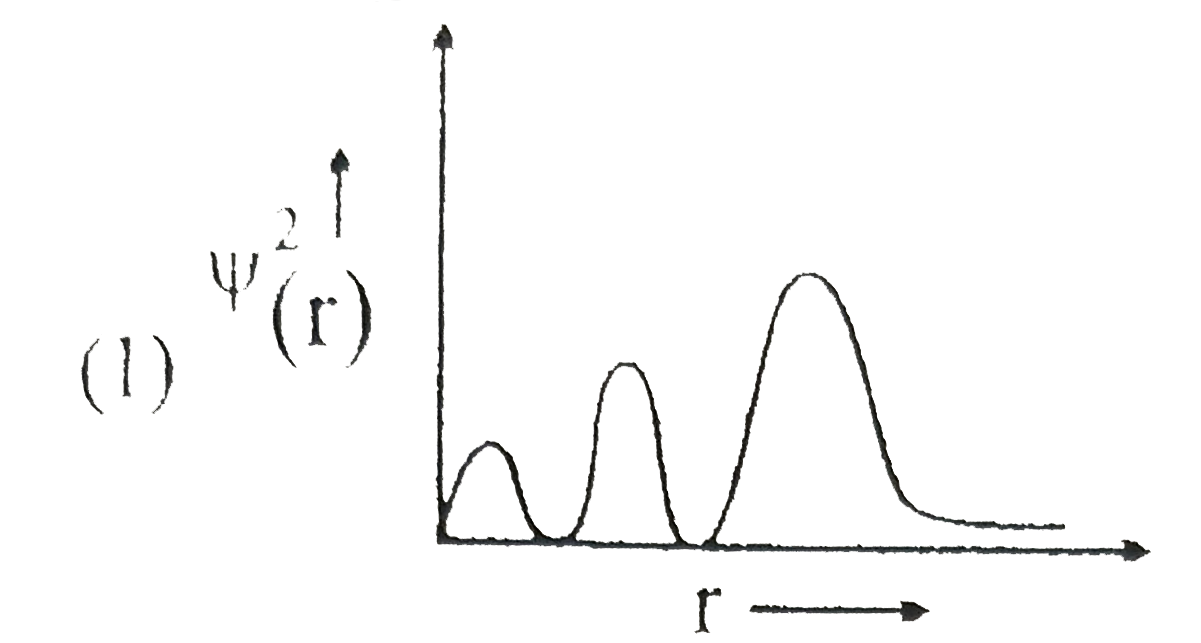 B
B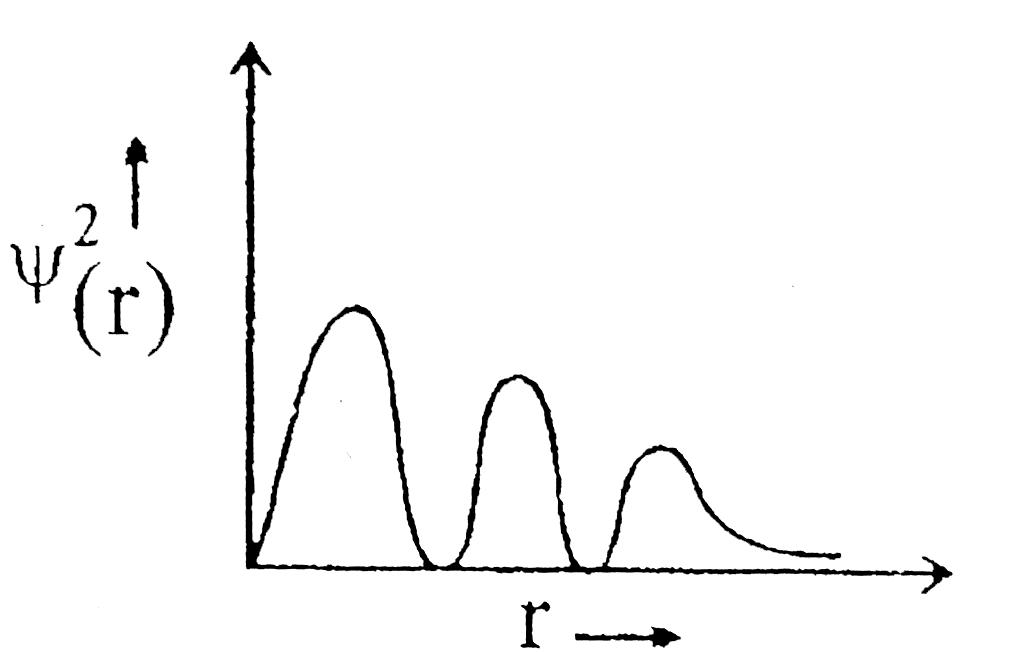 C
C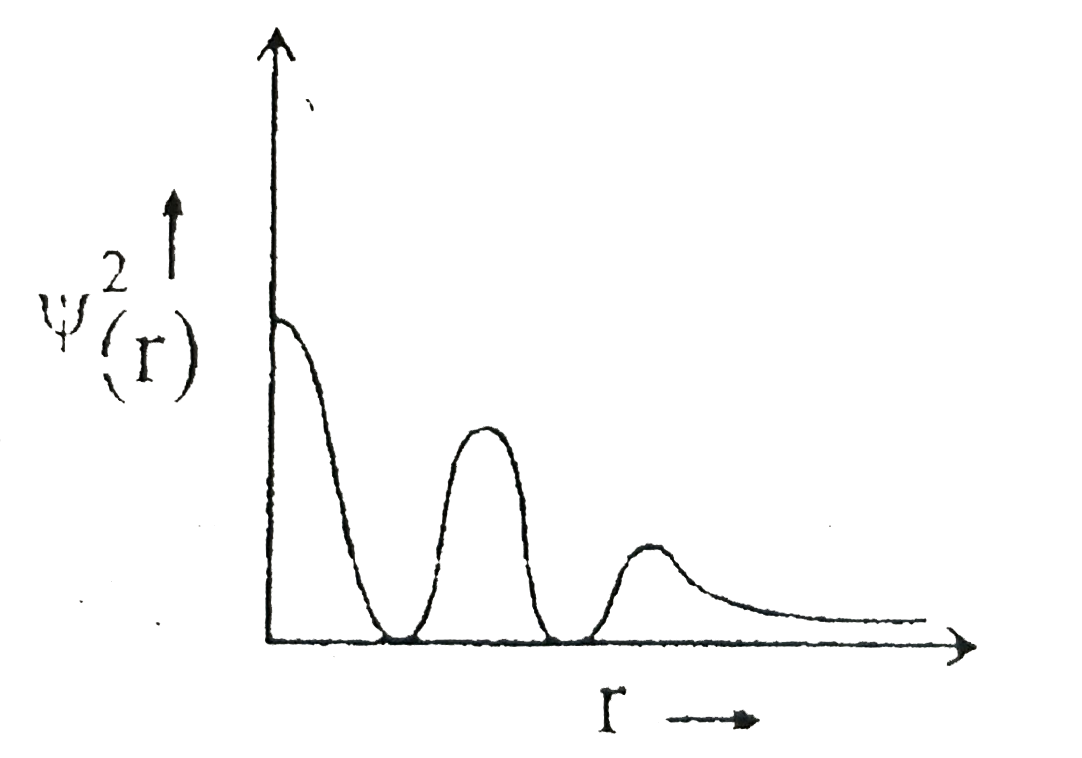 D
D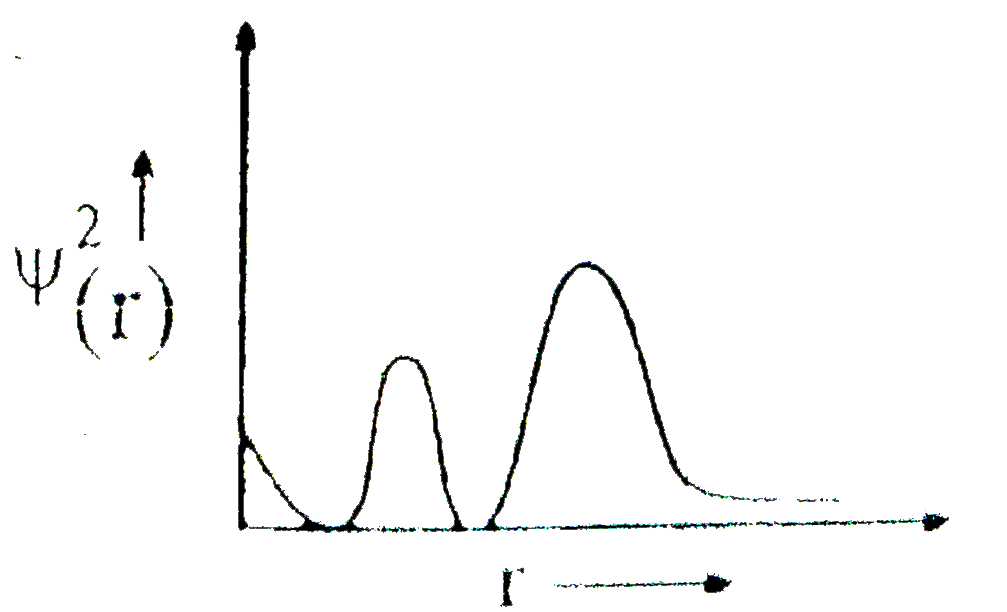
For which of the following orbitals is the radial probaility density R2 the maximum at the nucleus and descrease sharply as the distance form the nucleus increases?
A1sB2sC3sDAll the s orbitals
Radial probability density function || Illustration OF Radial probability density function
View SolutionIf P(r) is the radial probability density for a hydrogen atom then the probability that the separation of the electron and proton is between r and r+ dr is
View SolutionFor a mutielectron atom, the maximum of 2p-orbital in radial probability distribution graph is nearer the nucleus than that of 2s-orbital . Therefore, 2p-orbital should be closer to the nucleus and lower in energy than 2s-orbital. But 2s-orbital has lower energy than 2p-orbital. Explain.
View SolutionHow many times is the distance of maximum probability of 2p electron from the nucleus as compared to Bohr radius ?
View SolutionThe maximum radial probability in 1s-orbital occures at a distance when : [r0=Bohr radius]
View Solution

