Total number of isomers of [Co(en)2CI2]+ is
A
3
B
4
C
2
D
5
Video Solution
Text Solution
The correct Answer is:A
Ethylenediamine (or any bidentate ligand) always spans adjacent corner of an octahedron, but tge C1− ligands can be on either adjacent or opposite corners. Therefore there are two diastereoisomers, cis trans :
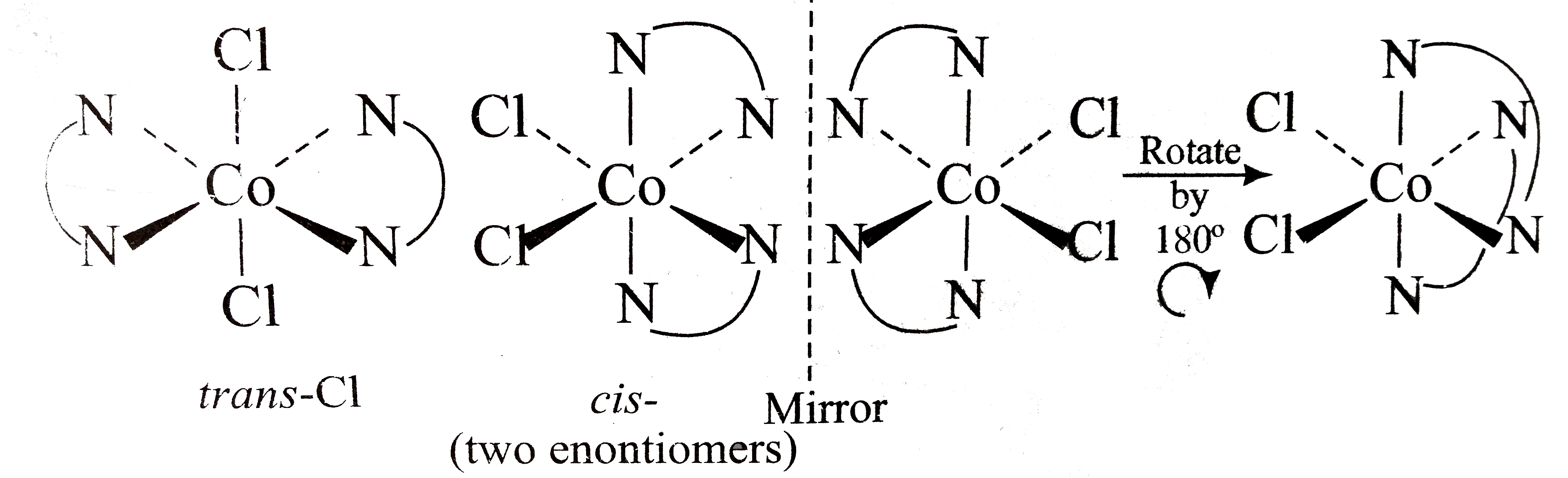
Because the trans isomer has several symmetry plane-one cuts through the Co and the en ligands -it is achrial and has no enantiomers. However, the cis isomer is chiral and exists as a pair of enantiomers that are non identical mirror images. We can see that the cis enantiomer on the right is not the same as the one the left if we rotate it by 180∘ about the vertical N-Co-N Axis.
|
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - R SHARMACHAPTER - COORDINATION COMPOUNDSEXERCISE - Question Bank (Building the knowledge)
38 Videos
- COORDINATION COMPOUNDSBOOK - R SHARMACHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives
56 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - R SHARMACHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - Archives
11 Videos
- ELECTROCHEMISTRYBOOK - R SHARMACHAPTER - ELECTROCHEMISTRYEXERCISE - Follow-up Test 11
7 Videos
Similar Questions
Knowledge Check
Assertion The total number of isomers shown by [Co(en)2CI2]⊕ complex ion is three
[Co(en)2CI2]2+ complex ion has an octahedral geometry .AIf both (A) and (R) are correct and (R) is the correct explanation of (A) .BIf both (A) and (R) are correct and (R) is the correct explanation of (A) .CIf(A) is correct, but (R) is incorrect .DBoth (A) and (R) are incorrect .Total number of ionisation isomers of [Co(en)2(Br)(Cl)]NO3 are (including the given compound)
A3B4C5D9The total number of optically active isomers of [Pt(en)2Cl2]2+ is :
A2B3C4D6
Give the number of possibel isomers of
[CrCI2en2]⊕ .
View SolutionThe total number of optically active isomers of [Pt(en)2Cl2]2+ is :
View SolutionThe possible number of the optical isomers in [Cr(en)2CI2]⊕ is .
View SolutionThe total number of isomer shown by [Co(NH3)4(NO2)2](NO3) complex is :
View SolutionThe number of possible isomers [Pt(en)(NO2)2]
View Solution
