Whenever two-demiensional square packing same layers are kept in the way so that the centres are aligned in all three dimensation, coordination numberof each sphere is
6
8
12
10
The correct Answer is:A
a. The coordination number is 6.(4 atoms in the plane +1 atom above +1 atoms below the particular atom).
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
3 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRYCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
Knowledge Check
When over a two-dimensional square packing same layers are kept in the way so that the centers are alligned in all three dimensions, coordination number of each sphere is
A6B8C12D10In hcp arrangment in three dimensions, the overall coordination number of each sphere is
A4B6C9D12In hexagonal closest-packed arrangement each spher has a coordinationnumber of
A4B6C8D9
What is the two-dimensional coordination number of a molecule in square close-packed layer?
View SolutionWhat is the two dimensional coordination number of a molecule in square close-packed layer ?
View SolutionMatch the type of packing given in column I with the iterms given in column II.
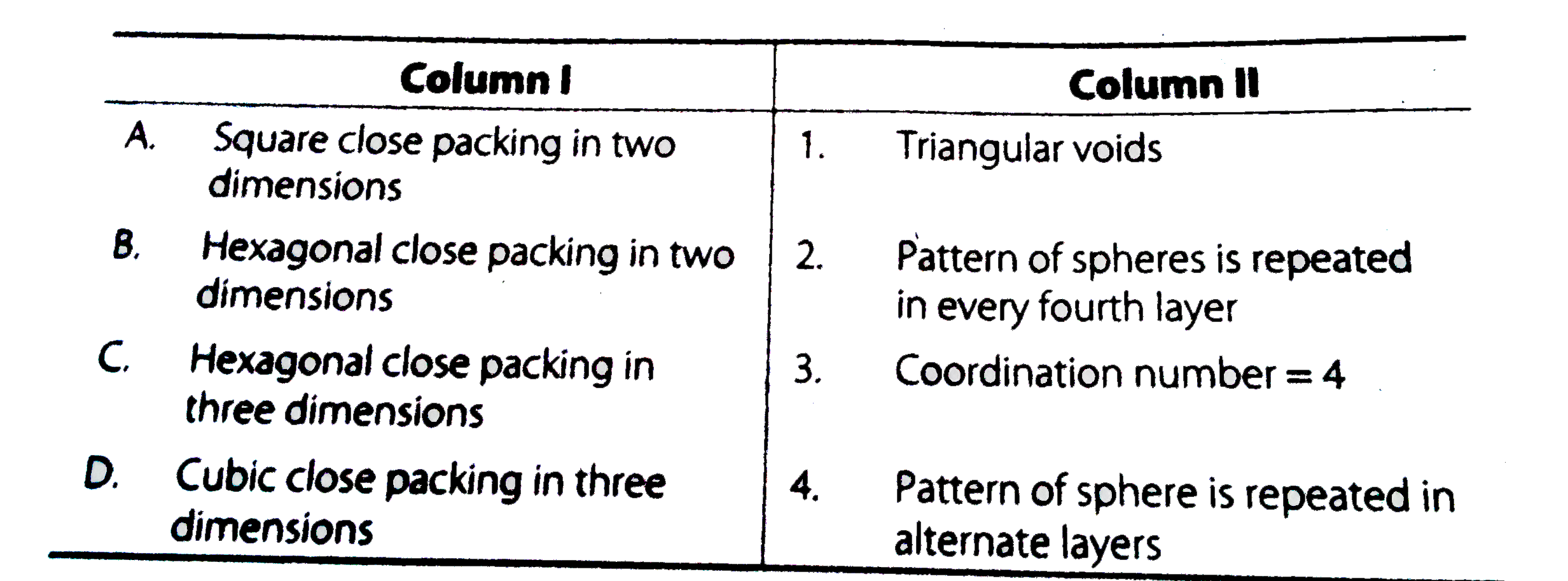
View SolutionIn a hexagonal closest packing in two layers one above the other, the coordiantion number of each sphere will be
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
What will be the ratio of radii of the spheres in cubic systems simple cubic, body centred cubic and face centred cubic systems. if 'a' stands for the edge length.
View Solution
