Which Nernst equation is true to find out the potential of non-standard electrochemical cell from the following ?
$F e (s) ∣ ∣ F e^{2 +} (x M) ∣ ∣ ∣ I^{-} (s) (P t)$

A

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{0.592}{n} {log}_{10} [F e^{2 +}] {[I^{-}]}^{2}$

B

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{0.0592}{n} {log}_{10} [F e^{2 +}] {[I^{-}]}^{2}$

C

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{0.0592}{n} {log}_{10} [F e^{2 +}] [I^{-}]$

D

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{0.0592}{n F} {log}_{10} . \frac{[F e^{2 +}] {[I^{-}]}^{2}}{[F e] [I_{2}]}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the potential of the non-standard electrochemical cell represented by the notation $F e (s) ∣ ∣ F e^{2 +} (x M) ∣ ∣ ∣ I^{-} (s) (P t)$ , we can use the Nernst equation. Here’s a step-by-step solution:
Step 1: Identify the half-reactions
In the given cell, we have:
- Oxidation half-reaction:
$Fe(s) \to {Fe}^{2 +} + 2 e^{-}$
- Reduction half-reaction:
$I_{2} + 2 e^{-} \to 2 I^{-}$
Step 2: Write the overall cell reaction
Combining the half-reactions, we get the overall cell reaction:
$Fe(s) + I_{2} \to {Fe}^{2 +} + 2 I^{-}$
Step 3: Write the Nernst equation
The Nernst equation relates the cell potential (E) to the standard cell potential (E°) and the concentrations of the reactants and products:
$E = E^{\circ} - \frac{0.0591}{n} log Q$
where:
- $E$ = cell potential
- $E^{\circ}$ = standard cell potential
- $n$ = number of moles of electrons transferred (which is 2 in this case)
- $Q$ = reaction quotient
Step 4: Determine the reaction quotient (Q)
For the reaction:
$Fe(s) + I_{2} \to {Fe}^{2 +} + 2 I^{-}$
The reaction quotient $Q$ is given by:
$Q = \frac{({Fe}^{2 +})}{(I_{2})}$
Since the solid iron (Fe) does not appear in the expression, we only consider the aqueous ions.
Step 5: Substitute values into the Nernst equation
Substituting the values into the Nernst equation:
$E = E^{\circ} - \frac{0.0591}{2} log (\frac{({Fe}^{2 +})}{(I_{2})})$
Final Nernst Equation
Thus, the Nernst equation to find the potential of the non-standard electrochemical cell is:
$E = E^{\circ} - 0.02955 log (\frac{({Fe}^{2 +})}{(I_{2})})$

Updated on:7/8/2024

|

Class 12 CHEMISTRY ELECTROCHEMISTRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

What is the $Δ G^{\circ}$ value for the electrochemical cell below?
$C u (s) ∣ ∣ C u^{2 +} (a q) ∣ ∣ ∣ ∣ N O_{3}^{-} (a q) ∣ ∣ N O (s) ∣ P t (s)$

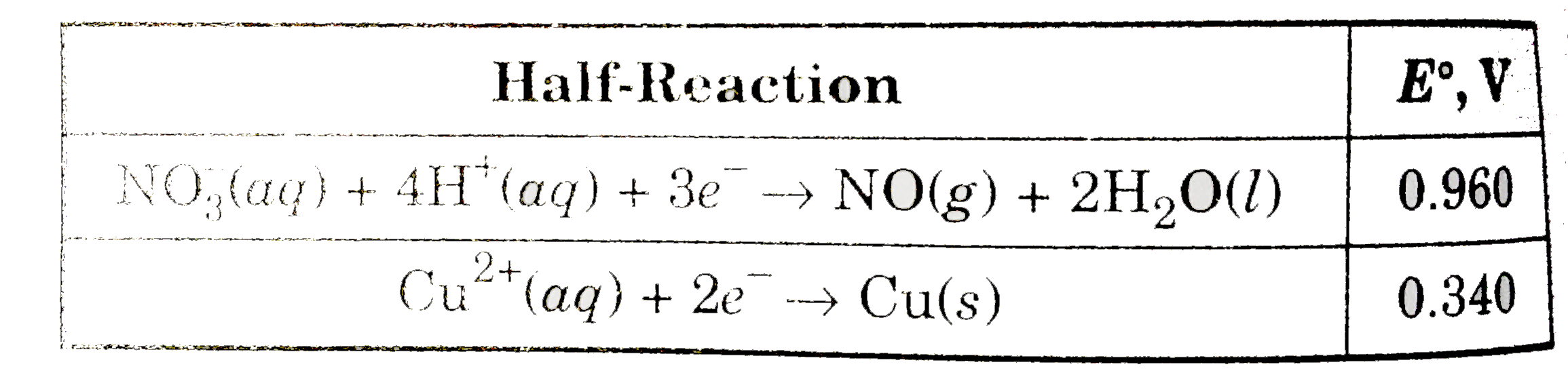A $- 753$ kJ
B $- 359$ kJ
C $- 179$ kJ
D $- 59.8$ kJ
At $25^{\circ} C$ temperature the cell potential of a given electrochemical cell is 1.92 V
$M g (s) ∣ ∣ M g^{2 +} (A q) x M ∣ ∣ ∣ ∣ F e^{2 +} (a q) 0.01 M ∣ ∣ F e (s)$
Given $E_{M g / m g^{2 +}}^{2 +} (A q) = 2.37 v$
$E_{F e / F e^{2 +}}^{\circ} (A q) = 0.45 V$ Find the value of x
A $x = 0.01 M$
B $x < 0.01 M$
C $x > 0.01 M$
Dx cannot be predicted

OP TANDON-ELECTROCHEMISTRY-OBJECTIVE TYPE QUESTION (LEVEL -A)

Home
Ask Doubt
Profile