Which of the following are resolvable ?
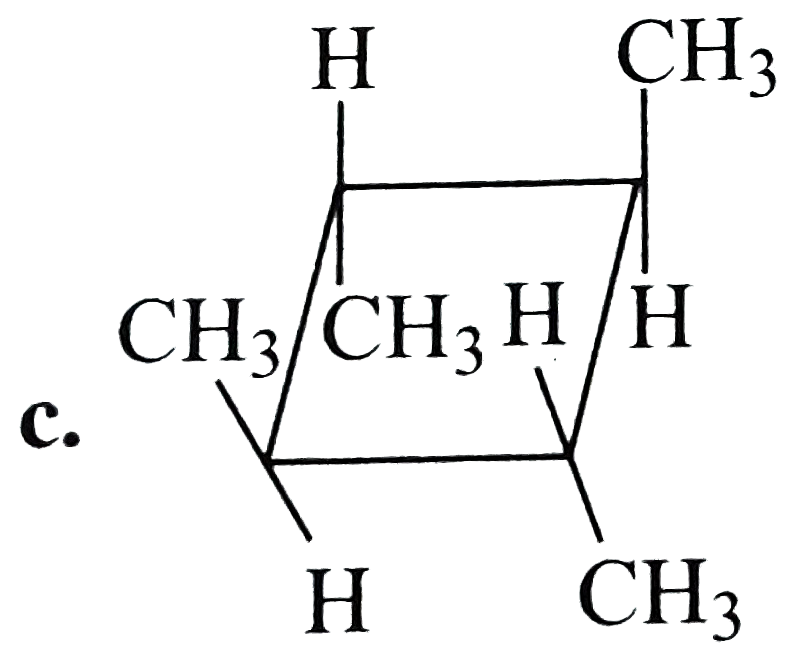
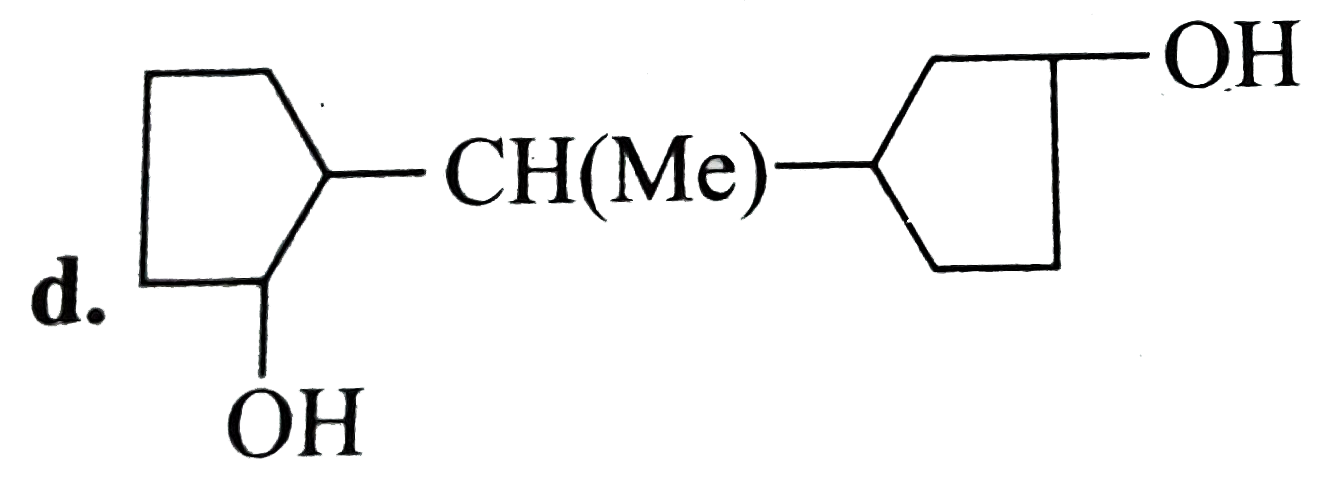
The correct Answer is:B, D
To determine which compounds are resolvable, we need to identify if they contain chiral carbon atoms. A chiral carbon atom is one that is attached to four different groups, making the compound optically active and thus resolvable. Let's analyze each option step by step.
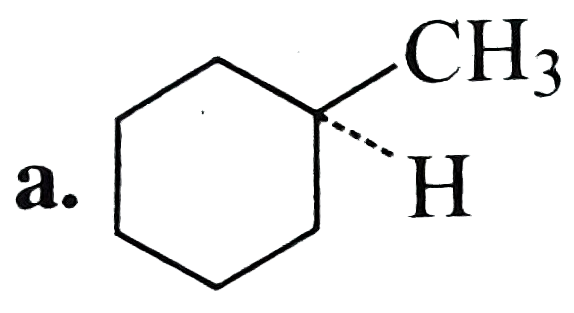
1. Option A:
- Draw the structure of the compound.
- Analyze the carbon atoms in the structure.
- Check if any carbon atom is attached to four different groups.
- Conclusion: The carbon atom in this compound is not chiral because it does not have four different substituents. Therefore, this compound is non-resolvable.
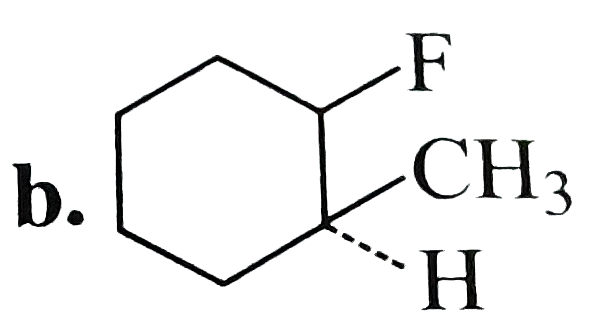
2. Option B:
- Draw the structure of the compound.
- Identify the carbon atom in question.
- Check the groups attached to this carbon atom.
- Conclusion: This carbon atom is chiral because it has four different groups attached (e.g., CH3, H, F, and another group). Hence, this compound is optically active and resolvable.
3. Option C:
- Draw the structure of the compound.
- Look for any planes of symmetry in the structure.
- Conclusion: This compound has a diagonal plane of symmetry, indicating that it is superimposable on its mirror image. Therefore, it is non-resolvable.
4. Option D:
- Draw the structure of the compound.
- Identify the carbon atom and the groups attached to it.
- Check if this carbon atom is chiral.
- Conclusion: This carbon atom is chiral as it is attached to four different groups (e.g., OH, H, and two other distinct groups). Thus, this compound is optically active and resolvable.
Final Answer:
The resolvable compounds are Option B and Option D.
- Draw the structure of the compound.
- Analyze the carbon atoms in the structure.
- Check if any carbon atom is attached to four different groups.
- Conclusion: The carbon atom in this compound is not chiral because it does not have four different substituents. Therefore, this compound is non-resolvable.
- Draw the structure of the compound.
- Identify the carbon atom in question.
- Check the groups attached to this carbon atom.
- Conclusion: This carbon atom is chiral because it has four different groups attached (e.g., CH3, H, F, and another group). Hence, this compound is optically active and resolvable.
- Draw the structure of the compound.
- Look for any planes of symmetry in the structure.
- Conclusion: This compound has a diagonal plane of symmetry, indicating that it is superimposable on its mirror image. Therefore, it is non-resolvable.
- Draw the structure of the compound.
- Identify the carbon atom and the groups attached to it.
- Check if this carbon atom is chiral.
- Conclusion: This carbon atom is chiral as it is attached to four different groups (e.g., OH, H, and two other distinct groups). Thus, this compound is optically active and resolvable.
The resolvable compounds are Option B and Option D.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Single correct answer type13videos
ISOMERISM
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Single correct answer type (Exercise)65videos
ISOMERISM
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - (Linked Comprehension Type)Exercise13videos
ISOMERISM
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Archives Subjective28videos
IONIC EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Chemical Equilibrium73videos
NCERT BASED EXERCISE
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following carboxylic acid could be resolved reaction with an enantiomerically pure chiral amine ?
A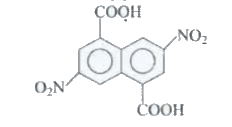 B
B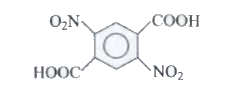 C
C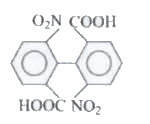 D
D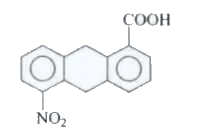
- Question 2 - Select One
Which of the following carboxylic acids could be resolved by reaction with an enantiomerically pure chiral amine ?
A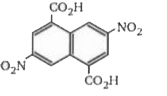 B
B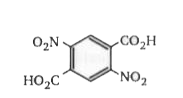 C
C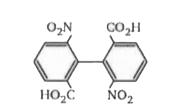 D
D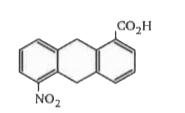
- Question 3 - Select One
Which of following compounds exists as non-resolvable racemic mixture?
A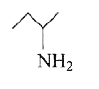 B
B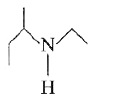 C
C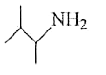 D
D
Which of the following molecule can resolved into enantiomers ?
View SolutionWhich of the following compound can be resolved into enatiomers ?
View SolutionFind the number of ways in which the number 94864 can be resolved as a product of two factors.
View SolutionFind the number of ways in which the number 94864 can be resolved as a product of two factors.
View SolutionThe maximum number of rectangular components into which a vector in space can be resolved into is
View Solution

