Which of the following can show geometrical isomerism?
⎡⎢ ⎢⎣Pt⎛⎜ ⎜⎝NH2−C∣CH3H−C∣CH3H−NH2⎞⎟ ⎟⎠2⎤⎥ ⎥⎦2+
[Co(en)2NH3Cl]2+
Both (a) and (b)
none of these
The correct Answer is:B
To determine which of the following coordination compounds can show geometrical isomerism, we need to analyze the structures and the arrangement of ligands around the central metal ion. Geometrical isomerism occurs when ligands can be arranged in different spatial orientations, leading to distinct isomers, typically classified as cis and trans.
1. Understanding Geometrical Isomerism:
- Geometrical isomerism arises due to the different arrangements of ligands around a central metal ion. The two main types are:
- Cis Isomer: Similar ligands are on the same side.
- Trans Isomer: Similar ligands are on opposite sides.
2. Identifying the Coordination Compounds:
- We need to analyze the given coordination compounds. Let's consider two examples:
- Example 1: A complex with the formula (Pt(CH₃)₂Cl₂).
- Example 2: A complex with the formula (Co(en)Cl₂) (where en = ethylenediamine).
3. Analyzing Example 1: (Pt(CH₃)₂Cl₂)
- In this complex, there are two methyl (CH₃) groups and two chloride (Cl) ligands.
- Cis Isomer: Both CH₃ groups are on the same side of the platinum ion.
- Trans Isomer: The CH₃ groups are on opposite sides of the platinum ion.
- Therefore, this complex can exhibit geometrical isomerism.
4. Analyzing Example 2: (Co(en)Cl₂)
- Here, ethylenediamine (en) acts as a bidentate ligand, and there are two chloride (Cl) ligands.
- Cis Isomer: The two Cl ligands are adjacent to each other.
- Trans Isomer: The Cl ligands are on opposite sides of the cobalt ion.
- Thus, this complex can also exhibit geometrical isomerism.
5. Conclusion:
- Both complexes (Pt(CH₃)₂Cl₂) and (Co(en)Cl₂) can show geometrical isomerism due to the arrangement of their ligands around the central metal ion.
Final Answer:
Both the complexes (Pt(CH₃)₂Cl₂) and (Co(en)Cl₂) can show geometrical isomerism.
- Geometrical isomerism arises due to the different arrangements of ligands around a central metal ion. The two main types are:
- Cis Isomer: Similar ligands are on the same side.
- Trans Isomer: Similar ligands are on opposite sides.
- We need to analyze the given coordination compounds. Let's consider two examples:
- Example 1: A complex with the formula (Pt(CH₃)₂Cl₂).
- Example 2: A complex with the formula (Co(en)Cl₂) (where en = ethylenediamine).
- In this complex, there are two methyl (CH₃) groups and two chloride (Cl) ligands.
- Cis Isomer: Both CH₃ groups are on the same side of the platinum ion.
- Trans Isomer: The CH₃ groups are on opposite sides of the platinum ion.
- Therefore, this complex can exhibit geometrical isomerism.
- Here, ethylenediamine (en) acts as a bidentate ligand, and there are two chloride (Cl) ligands.
- Cis Isomer: The two Cl ligands are adjacent to each other.
- Trans Isomer: The Cl ligands are on opposite sides of the cobalt ion.
- Thus, this complex can also exhibit geometrical isomerism.
- Both complexes (Pt(CH₃)₂Cl₂) and (Co(en)Cl₂) can show geometrical isomerism due to the arrangement of their ligands around the central metal ion.
Both the complexes (Pt(CH₃)₂Cl₂) and (Co(en)Cl₂) can show geometrical isomerism.
Topper's Solved these Questions
- CO-ORDINATION COMPOUNDSBOOK - VK JAISWAL ENGLISHCHAPTER - CO-ORDINATION COMPOUNDSEXERCISE - SUBJECTIVE PROBLEMS
42 Videos
- CHEMICAL BONDING (BASIC)BOOK - VK JAISWAL ENGLISHCHAPTER - CHEMICAL BONDING (BASIC)EXERCISE - SUBJECTIVE PROBLEMS
54 Videos
- d-BLOCK ELEMENTSBOOK - VK JAISWAL ENGLISHCHAPTER - d-BLOCK ELEMENTSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
32 Videos
Similar Questions
Knowledge Check
Which of the following will not show geometrical isomerism ?
A B
B C
C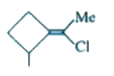 D
D
Which of the following will not show geometrical isomerism?
A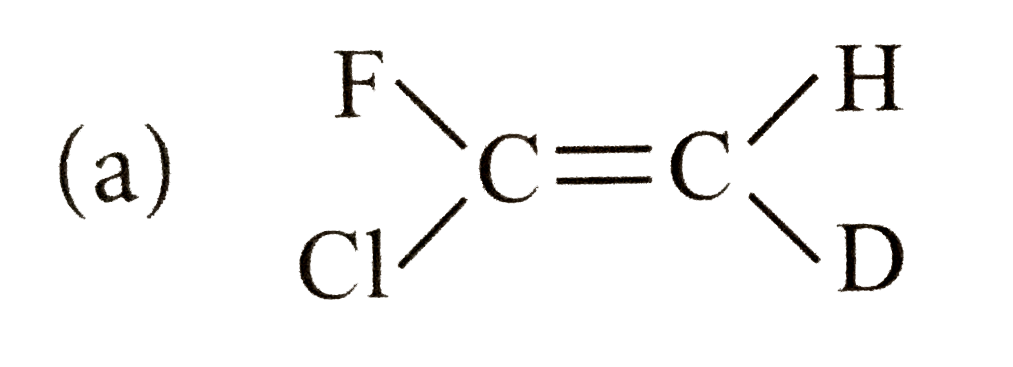 B
B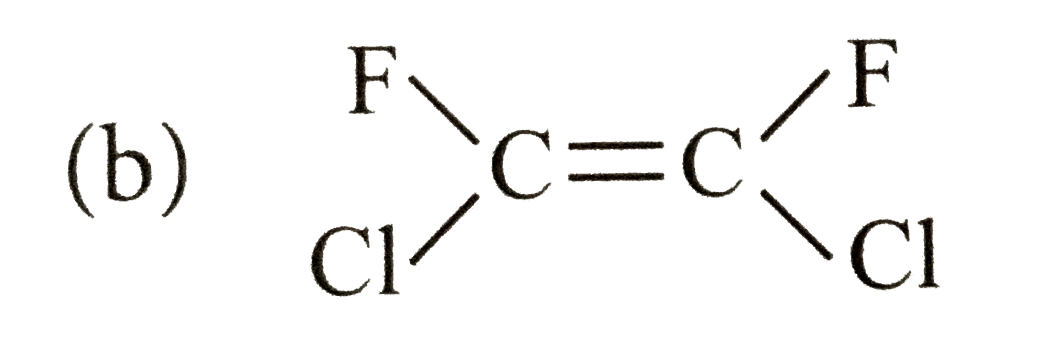 C
C D
D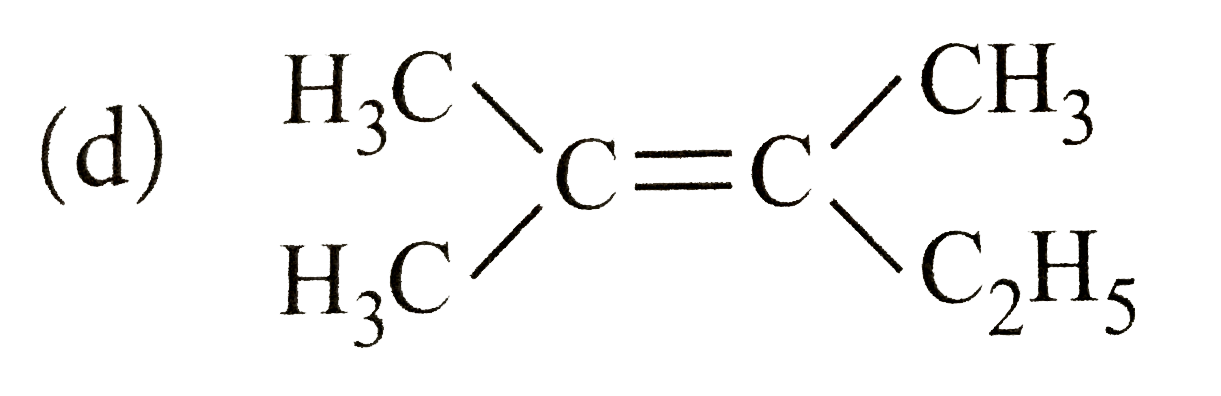
Which of the folllowing shows geometrical isomerism ?
View SolutionWhich of the following can exhibit geometrical isomerism?
View SolutionWhich of the following will not show geometrical isomerism ?
View SolutionWhich of the following will not show geometrical isomerism?
View SolutionWhich of the following will not show geometrical isomerism?
View SolutionWhich of the following will not show geometrical isomerism?
View Solution
