Which of the following connot be obtained form the solution of Schrodinger wave equation ?
Wave function of an electron
Energy of an elecrtron in a 1−D box
Energyof an electron in orbitals
Velocity of electron in circular orbits
The correct Answer is:D
To solve the question "Which of the following cannot be obtained from the solution of the Schrödinger wave equation?", we need to analyze the options provided in relation to what the Schrödinger equation can yield.
1. Understanding the Schrödinger Wave Equation:
The Schrödinger wave equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes over time. The equation is given by:
∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2+8π2mh2(E−V)ψ=0
Here, ψ is the wave function, E is the total energy, V is the potential energy, and m is the mass of the particle.
2. Identifying the Options:
The options provided in the question are:
- A) Wave function of electron
- B) Energy of an electron in a 1D box
- C) Energy of an electron in orbitals
- D) Velocity of an electron in circular orbits
3. Analyzing Each Option:
- Option A (Wave function of electron): This can be obtained directly from the Schrödinger equation as it is the primary output of the equation.
- Option B (Energy of an electron in a 1D box): This can also be derived from the Schrödinger equation for a particle in a box scenario.
- Option C (Energy of an electron in orbitals): The energies associated with orbitals can be determined from the solutions of the Schrödinger equation for hydrogen-like atoms.
- Option D (Velocity of an electron in circular orbits): The Schrödinger equation does not provide a direct value for velocity. Instead, it gives the probability distribution of finding an electron in a certain position, not its velocity.
4. Conclusion:
Based on the analysis, the option that cannot be obtained from the solution of the Schrödinger wave equation is:
D) Velocity of an electron in circular orbits.
Final Answer:
D) Velocity of an electron in circular orbits
The Schrödinger wave equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes over time. The equation is given by:
∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2+8π2mh2(E−V)ψ=0
Here, ψ is the wave function, E is the total energy, V is the potential energy, and m is the mass of the particle.
The options provided in the question are:
- A) Wave function of electron
- B) Energy of an electron in a 1D box
- C) Energy of an electron in orbitals
- D) Velocity of an electron in circular orbits
- Option A (Wave function of electron): This can be obtained directly from the Schrödinger equation as it is the primary output of the equation.
- Option B (Energy of an electron in a 1D box): This can also be derived from the Schrödinger equation for a particle in a box scenario.
- Option C (Energy of an electron in orbitals): The energies associated with orbitals can be determined from the solutions of the Schrödinger equation for hydrogen-like atoms.
- Option D (Velocity of an electron in circular orbits): The Schrödinger equation does not provide a direct value for velocity. Instead, it gives the probability distribution of finding an electron in a certain position, not its velocity.
Based on the analysis, the option that cannot be obtained from the solution of the Schrödinger wave equation is:
D) Velocity of an electron in circular orbits.
D) Velocity of an electron in circular orbits
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 3B
19 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise 4
39 Videos
- ATOMIC STRUCTUREBOOK - P BAHADURCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercise
19 Videos
- CHEMICAL BONDINGBOOK - P BAHADURCHAPTER - CHEMICAL BONDINGEXERCISE - Exercise 7
11 Videos
Similar Questions
Knowledge Check
Which of the following is obtained form coal tar?
APetrolBCokeCAirDNaphthalene ballsIn the Schrodinger equation, H is
Aa mathematical operator called HamiltonianBconstructed by Schrodinger from the expression for the total energy of the systemCBoth (1) and (2)DNeither (1) nor (2) trueThe quantum number not obtained from the schrodinger's wave equation is
AnBlCmDs
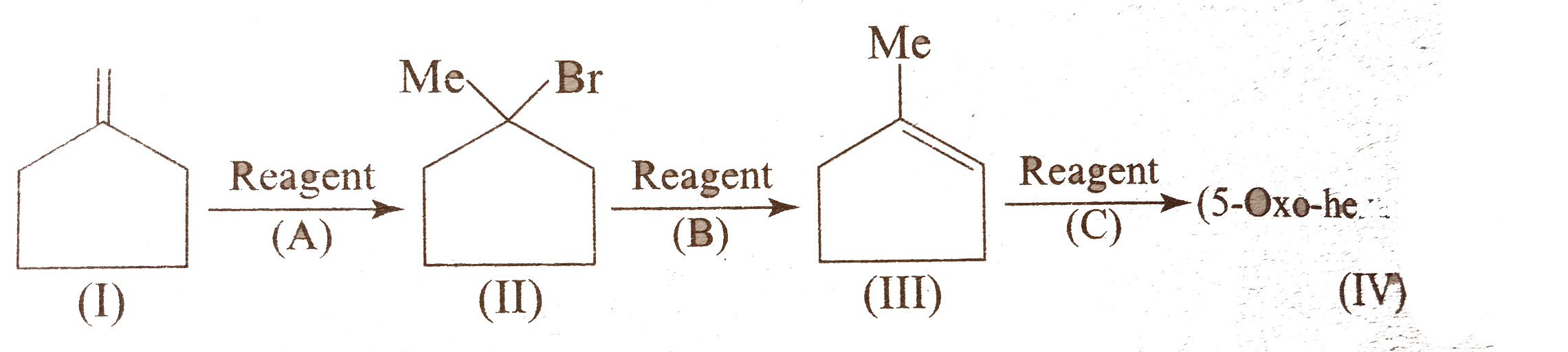
Which of the following connot be used as reagent (B) ?
View SolutionWhich of the following compounds is NOT obtained in the solid form ?
View SolutionWhich of the following quantum number has not been derived from Schrodinger wave equation.
View SolutionThe quantum number not obtained from the schrodinger's wave equation is
View SolutionWhich of the following forms ideal solution?
View Solution
