X is a pale yellow solid. It hydrolyses to POCl3 in moist air and finally gets converted into phosphoric acid. Z exists as an ionic solid. The total number of atoms present in its cation is.
The correct Answer is:5
PCl5(X)+H2O→POCl3+2HCl,
POCl3+3H2O→H3PO4+3HCl
In the solid state, PCl5 (X) exists as [PCl4]+[PCl6]− in which the cation has 5 atmos (4Cl+1P).
Topper's Solved these Questions
- P-BLOCK ELEMENTS (NITROGEN FAMILY)BOOK - PRADEEPCHAPTER - P-BLOCK ELEMENTS (NITROGEN FAMILY)EXERCISE - Competition focus jee(main and advanced)/ medical entrance special) (VII. Numerical Value Type Questions (In Decimal Notation))
1 Videos
- P-BLOCK ELEMENTS (NITROGEN FAMILY)BOOK - PRADEEPCHAPTER - P-BLOCK ELEMENTS (NITROGEN FAMILY)EXERCISE - Competition focus jee(main and advanced)/ medical entrance special) (VIII. Assertion-Reason Type Questions)
10 Videos
- P-BLOCK ELEMENTS (NITROGEN FAMILY)BOOK - PRADEEPCHAPTER - P-BLOCK ELEMENTS (NITROGEN FAMILY)EXERCISE - Competition focus jee(main and advanced)/ medical entrance special) (V. matrix-match Type Questions)
2 Videos
- ORGANIC CHEMISTRY-SOME BASIC PRINCIPLES TECHNIQUESBOOK - PRADEEPCHAPTER - ORGANIC CHEMISTRY-SOME BASIC PRINCIPLES TECHNIQUESEXERCISE - Competition Focus (Jee (Main and Advanced)/Medical Entrance) VIII. Assertion-Reason Type Questions
25 Videos
- REDOX REACTIONS BOOK - PRADEEPCHAPTER - REDOX REACTIONS EXERCISE - Assertion reason type question
16 Videos
Similar Questions
X is a pale yellow solid. It hydrolyses to POCl3 in moist air and finally gets converted into phosphoric acid. Z exists as an ionic solid. The total number of atoms present in its cation is.
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
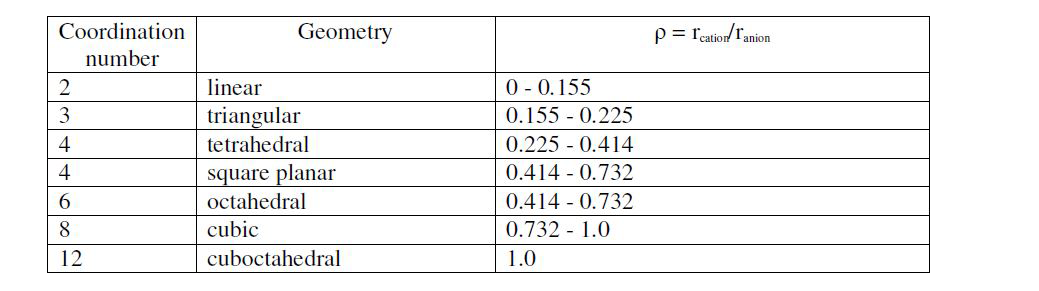
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−
View Solution
Knowledge Check
Two substances X and Y are dissolved in water under suitable conditions. X is a gas while Y is a solid under normal conditions. Solution of Y is found to conduct electricity but not 'X'. Based on the conclusion identify the nature of bond present in X and Y with appropriate reasons as given below.
Arrange the steps given below in a sequence.
(1) Y is a solid at room temperature and its aqueous solution conducts electricity. This shows that it is an ionic compound.
(2) X on dissolution in water does not conduct electricity and is a gas at room temperature. Hence it should be a non-polar covalent molecule.
(3) Aqueous solutions of both ionic compounds and polar covalent compounds conduct electricity because of the presence of free ions.
(4) All ionic compounds are solids and most of the non-polar covalent molecules are gases or solids at room temperature. Polar covalent compounds are liquids or gases.A3 4 2 1B1 4 3 2C1 3 2 4D3 1 2 4In chemistry, 'mole' is an essential tool for the chemical calculations. It is a basic SI unit adopted by the 14th general conference on weights and measurements in 1971. A mole contains as many elementary particles as the number of atoms present in 12 g of 12C . 1 mole of a gas at STP occupies 22.4 litre volume. Molar volume of solids and liquids is not definite. Molar mass of a substance is also called gram-atomic mass or gram molecular mass. The virtual meaning of mole is plenty, heap or the collection of large numbers. 1 mole of a substance contains 6.022×1023 elementary particles like atom or molecule. Atomic mass unit (amu) is the unit of atomic mass, e.g., atomic mass of single carbon is 12 amu.
XL N2 , gas at STP contains 3×1022 molecules. The number of molecules in x L ozone at STP will beA3×1022B4×1023C6.02×1023D3×1024In chemistry, 'mole' is an essential tool for the chemical calculations. It is a basic SI unit adopted by the 14th general conference on weights and measurements in 1971. A mole contains as many elementary particles as the number of atoms present in 12g of .12C. 1 mole of a gas at STP occupies 22.4 litre volume. molar volume of solids and liquids is not definite Molar mass of a substance is also called gram-atomic mass or gram molar mass. the virtual meaning of mole is plenty. heap of the collection of large numbers. 1 mole of a substance contains 6.023×1023 elementary particles like atom or molecule. Atomic mass unit (amu) is the unit of atomic mass, e.g., atomic mass of single carbon is 12 amu.
xL N2 gas at STP contains 3×1022 molecules. the number of molecules. in x L ozone at STP will be:A3×1022B6.02×1023C3×1024Dnone of these.
Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
A "good fit" is considered to be one where the cation can touch:
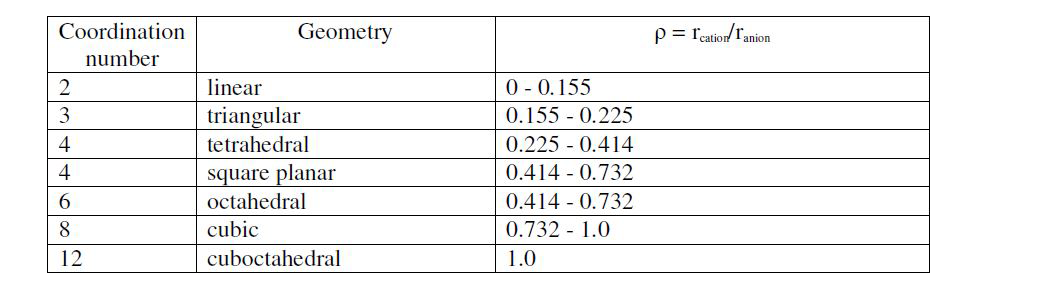
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.

The radius of Ag+ ion is 126pm and of I− ion is 216pm. The coordination number of Ag+ ion is:
View SolutionMonosaccharides are polyhydric aldehydes and ketones which cannot be hydrolysed into simpler carbohydrates. The monosaccharides containing −CHO group are called aldoses while those containing C=O group are called ketoses. The aldehyde group is always present at C1 while keto group is generally present at C2. All monosaccharides are oxidised by Tollen's reagent and Fehling solution and are called reducing sugars.
The monosaccharide molecules may be assigned D and L-configurations depending upon whether the configuration of the molecule is related to D- or L-glyceraldehyde. If the −OH group is attached to the carbon adjacent to the −CH2OH group (last chiral carbon) is on the right hand side, it is assigned D-configuration. The molecule is assigned L-configuration if the -OH group attached to the carbon adjacent to the −CH2OH group is on the left. The monosaccharides contain one or more chiral carbon atoms. Pentoses and hexoses have cyclic structures furanose (five membered) and pyranose (six membered). During cyclization, C1 in aldohexoses and C2 in fructose become chiral and the newly formed -OH group may be either on the left or on the right in Fischer projection formulae. These monosaccharides, therefore, exist in two stereoisomeric forms called α-anomer and β-anomer while C1andC2 are called glycosidic or anomeric carbon. The bonds joining glycosidic carbon are called glycosidic linkages. D(+) glucose exists in two stereoisomeric forms, α-D- glucose and β-D-glucose. When either of these two forms of glucose i.e., α−D−glucose are dissolved in water and allowed to stand, these get slowly converted into other form and an equilibrium mixture of both is formed. This process is called mutarotation.
The maximum number of optical isomers of glucose expected are
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
A solid AB has square planar structure. If the radius of cation A+ is 120 pm, calculate the maximum possible value of anion B−.
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
The radius of Ag+ ion is 126 pm and of I− ion is 216 pm. The coordination number of Ag+ ion is :
View Solution
