XA and XB are the mole fraction of A and B respectively in liquid phase yA and yB are the mole fraction of A and B respective in vapour phase. Find out the slope of straight line if a graph is plotted 1yA along Y-axis against 1xA along X-axis gives straight line [p∘A and p∘B are vapour pressure of pure components A and B].
P∘BP∘A
P∘AP∘B
P∘B−P∘A
P∘A−P∘B
The correct Answer is:a
To find the slope of the straight line when plotting 1yA against 1xA, we will follow these steps:
Step 1: Understand the relationship between mole fractions and partial pressures
The mole fraction of component A in the vapor phase, yA, can be expressed in terms of the partial pressure of A, PA, and the total pressure P:
yA=PAP
where P=PA+PB.
Step 2: Express the partial pressure PA
The partial pressure PA can be expressed as:
PA=xA⋅P0A
where P0A is the vapor pressure of pure component A, and xA is the mole fraction of A in the liquid phase.
Step 3: Substitute PA into the equation for yA
Substituting PA into the equation for yA:
yA=xA⋅P0AxA⋅P0A+xB⋅P0B
Since xB=1−xA, we can rewrite it as:
yA=xA⋅P0AxA⋅P0A+(1−xA)⋅P0B
Step 4: Simplify the expression for yA
This simplifies to:
yA=xA⋅P0AxA⋅P0A+P0B−xA⋅P0B
yA=xA⋅P0AxA(P0A−P0B)+P0B
Step 5: Take the reciprocal of yA
Taking the reciprocal gives:
1yA=xA(P0A−P0B)+P0BxA⋅P0A
Step 6: Rearrange the equation
Rearranging the equation:
1yA=(P0A−P0B)P0A+P0BxA⋅P0A
This can be expressed in the form of a straight line equation y=mx+c, where:
- y=1yA
- x=1xA
- Slope m=P0BP0A
Step 7: Conclusion
Thus, the slope of the straight line when plotting 1yA against 1xA is:
Slope=P0BP0A
The mole fraction of component A in the vapor phase, yA, can be expressed in terms of the partial pressure of A, PA, and the total pressure P:
yA=PAP
where P=PA+PB.
The partial pressure PA can be expressed as:
PA=xA⋅P0A
where P0A is the vapor pressure of pure component A, and xA is the mole fraction of A in the liquid phase.
Substituting PA into the equation for yA:
yA=xA⋅P0AxA⋅P0A+xB⋅P0B
Since xB=1−xA, we can rewrite it as:
yA=xA⋅P0AxA⋅P0A+(1−xA)⋅P0B
This simplifies to:
yA=xA⋅P0AxA⋅P0A+P0B−xA⋅P0B
yA=xA⋅P0AxA(P0A−P0B)+P0B
Taking the reciprocal gives:
1yA=xA(P0A−P0B)+P0BxA⋅P0A
Rearranging the equation:
1yA=(P0A−P0B)P0A+P0BxA⋅P0A
This can be expressed in the form of a straight line equation y=mx+c, where:
- y=1yA
- x=1xA
- Slope m=P0BP0A
Thus, the slope of the straight line when plotting 1yA against 1xA is:
Slope=P0BP0A
Topper's Solved these Questions
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-02
26 Videos
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-03
23 Videos
- CHEMICAL EQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Match the column
1 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
Similar Questions
For a ideal liquid solution with P∘A>P∘B, which relation betweenXA ((mole fraction of A in liquid phase) and YA(mole fraction of A in vapour phase) is correct ?
View SolutionPAandPB are the vapour pressure of pure liquid components ,Aand B respectively of an ideal binary solution,If xA represents the mole fraction of component A, the total pressure of the solution will be
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
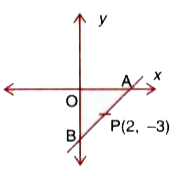
slope of line AB
View SolutionIf Pa and Pb are 108 and 36 torr respectively. What will be the mole fraction of A is vapour phase if B has mole fraction in solution 0.5:
View SolutionPA=(235y−125xy)mm of HgPA is partial pressure of A,x is mole fraction of B in liquid phase in the mixture of two liquids A and B and y is the mole fraction of A in vapour phase, then P∘B in mm of Hg is:
View SolutionFor an ideal binary liquid solutions with P∘A>P∘B, which relation between χA (mole fraction of A in liquid phase) and YA (mole fraction of A in vapour phase) is correct :
View SolutionIf two substances A and B have p∘A:p∘B=1:2 and have mole fraction in solution as 1:2 then mole fraction of A in vapour phase is
View SolutionA certain ideal solution of two liquids A and B has mole fraction of 0.3 and 0.5 for the vapour phase and liquid phase, respectively. What would be the mole fraction of B in the vapour phase, when the mole fraction of A in the liquid is 0.25?
View SolutionA mixture of two immiscible liquids A and B, having vapour pressure in pure state obeys the following relationship if χA and χB are mole fractions of A and B in vapour phase over the solution
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

equation of line AB.
View Solution
