Question

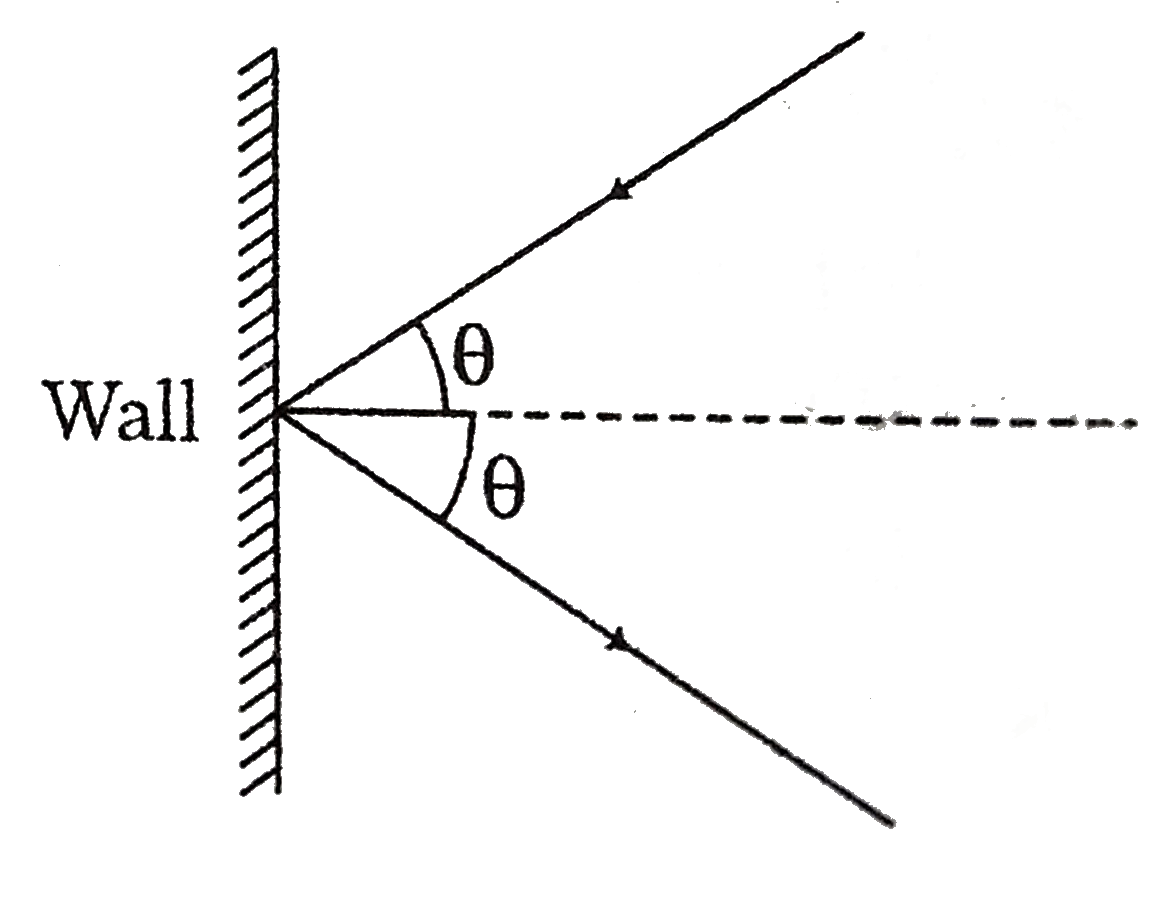
${10}^{23}$ molecules of a gas, each having a mass of $3\times {10}^{-27}$ kg strike per second per sq. cm. of a rigid will at an angle of ${60}^{\circ }$ with the normal and rebound with a velocity of $500m/s$. What is the pressure exerted by the gas molecules on the wall?

Options

A. `500N//m^(2)`
B. `1000N//m^(2)`
C. `1500N//m^(2)`
D. `2000N//m^(2)`

Answer

C

Explanation

To find the pressure exerted by the gas molecules on the wall, we can follow these steps:

Step 1: Understand the Given Information
We have:
- Number of molecules, \( N = 10^{23} \)
- Mass of each molecule, \( m = 3 \times 10^{-27} \) kg
- Velocity of molecules, \( v = 500 \) m/s
- Angle of incidence with the normal, \( \theta = 60^\circ \)

Step 2: Convert Mass Flow Rate to SI Units
The mass flow rate per unit area is given as \( 3 \times 10^{-27} \) kg/s/cm². We need to convert this to m²:
\( \text{Mass flow rate per unit area} = 3 \times 10^{-27} \, \text{kg/s/cm}^2 = 3 \times 10^{-27} \, \text{kg/s} \times 10^4 \, \text{cm}^{-2} = 3 \times 10^{-23} \, \text{kg/s/m}^2 \)

Step 3: Calculate the Change in Momentum for One Molecule
The change in momentum (\( \Delta p \)) for one molecule when it strikes the wall and rebounds is given by:
\( \Delta p = mv \cos(\theta) - (-mv \cos(\theta)) = 2mv \cos(\theta) \)
Substituting the values:
\( \Delta p = 2 \times (3 \times 10^{-27} \, \text{kg}) \times (500 \, \text{m/s}) \times \cos(60^\circ) \)
Since \( \cos(60^\circ) = \frac{1}{2} \):
\( \Delta p = 2 \times (3 \times 10^{-27}) \times 500 \times \frac{1}{2} = 3 \times 10^{-27} \times 500 = 1.5 \times 10^{-24} \, \text{kg m/s} \)

Step 4: Calculate the Total Change in Momentum for All Molecules
The total change in momentum per second (force) from all molecules is:
\( F = N \times \Delta p = 10^{23} \times 1.5 \times 10^{-24} = 1.5 \times 10^{-1} \, \text{N} \)

Step 5: Calculate the Pressure
Pressure (\( P \)) is defined as force per unit area. The area is \( 1 \, \text{m}^2 \):
\( P = \frac{F}{A} = \frac{1.5 \times 10^{-1} \, \text{N}}{1 \, \text{m}^2} = 0.15 \, \text{N/m}^2 = 150 \, \text{Pa} \)

Final Answer
The pressure exerted by the gas molecules on the wall is \( 150 \, \text{Pa} \).

---