20 J work is required to stretch a spring through 0.1 m . Find the force constant of the spring. If the spring is further stretched through 0.1 m. Calculate work done.
To solve the problem step by step, we will first find the spring constant (k) and then calculate the work done when the spring is further stretched.
Step 1: Calculate the spring constant (k)
The work done (W) on a spring when it is stretched is given by the formula:
W=12kx2
where:
- W is the work done (20 J in this case),
- k is the spring constant,
- x is the displacement (0.1 m).
Substituting the known values into the equation:
20=12k(0.1)2
Now, simplify the equation:
20=12k(0.01)
20=0.005k
To find k, rearrange the equation:
k=200.005
k=4000N/m
Step 2: Calculate the work done when the spring is further stretched
When the spring is further stretched through an additional 0.1 m, the total displacement becomes:
xtotal=0.1m+0.1m=0.2m
Now, we calculate the potential energy (U) at this new displacement using the same formula:
U=12kx2
Calculating U2 (potential energy when stretched to 0.2 m):
U2=12(4000)(0.2)2
U2=12(4000)(0.04)
U2=80J
We already calculated U1 (potential energy when stretched to 0.1 m) previously, which is 20 J.
Step 3: Calculate the work done (W)
The work done in stretching the spring from 0.1 m to 0.2 m is the change in potential energy:
W=U2−U1
W=80J−20J
W=60J
Final Answers:
- The spring constant k is 4000N/m.
- The work done in further stretching the spring through 0.1 m is 60J.
W=12kx2
where:
- W is the work done (20 J in this case),
- k is the spring constant,
- x is the displacement (0.1 m).
20=12k(0.1)2
20=12k(0.01)
20=0.005k
k=200.005
k=4000N/m
xtotal=0.1m+0.1m=0.2m
U=12kx2
U2=12(4000)(0.2)2
U2=12(4000)(0.04)
U2=80J
W=U2−U1
W=80J−20J
W=60J
- The spring constant k is 4000N/m.
- The work done in further stretching the spring through 0.1 m is 60J.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - WORK, ENERGY AND POWEREXERCISE - NUMERICALS
11 Videos
- WORK, ENERGY AND POWERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
20 Videos
- WORK, ENERGY AND POWERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
20 Videos
- THERMODYNAMICS BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - THERMODYNAMICS EXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
20 Videos
Similar Questions
A force of 1N is required to stretch a spring by 1.5cm. If the spring is cut into three equal parts, find the force required to stretch one part by 3 cm.
View SolutionConsider a block connected to a light spring of spring constant 100Nm−1. Now the block is displaced by applying a constant force F which gives zero resultant force when spring is stretched through 10 cm.
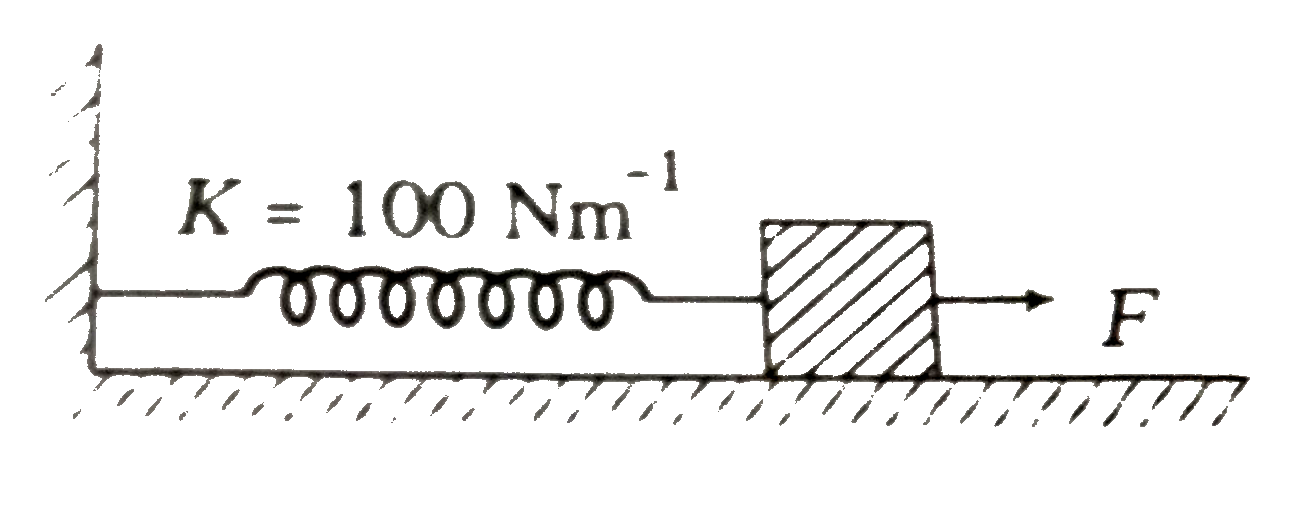
Evaluate
(i) Work done by the spring force when the block attains equilibrium.
(ii) Net work done on the block when it attains maximum speed.
View Solution
Knowledge Check
A mass of 1kg is hanged through a spring. The spring is stretched through 1cm. What is the energy stared in spring?
A0.449JB0.049JC4.9JD49JA mass of 1 kg is hanged through a spring. The spring is stretched through 1cm. What is the energy stared in spring?
A0.449JB0.049JC4.9JD49JAn elastic spring of unstretched length L and force constant k is stretched by a small length x. It is further stretched by another small length y. The work done in the second stretching is
A12ky2B12k(x2+y2)C12k(x+y)2D12ky(2x+y)
In the two block spring system, force constant of spring is k = 6N/m. Spring is stretched by 12 cm and then left. Match the following.

View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionThe work done in extending a spring by x0 is W0. Find the work done in further extension x0.
View SolutionA spring with spring constant k is extended from x=0 to x=x1. The work done will be
View SolutionA string of length L and force constant k is stretched to obtain extension l. It is further stretched to obtain extension l1. The work done in second streching is
View Solution
