220 V, 50 Hz , AC is applied to a resistor . The instantaneous value of voltage is
220√2sin100πt
220sin100πt
220√2sin50πt
220sin50πt
The correct Answer is:A
To find the instantaneous value of voltage when a 220 V, 50 Hz AC supply is applied to a resistor, we can follow these steps:
Step 1: Identify the RMS Voltage
The given RMS voltage (VRMS) is 220 V.
Step 2: Calculate the Peak Voltage (V0)
The peak voltage (V0) can be calculated using the relationship between RMS voltage and peak voltage:
V0=VRMS×√2
Substituting the given value:
V0=220V×√2≈220×1.414≈311.13V
Step 3: Determine the Angular Frequency (ω)
The angular frequency (ω) is related to the frequency (f) by the equation:
ω=2πf
Given that the frequency (f) is 50 Hz:
ω=2π×50Hz=100πrad/s
Step 4: Write the Equation for Instantaneous Voltage
The instantaneous voltage (V) as a function of time (t) can be expressed as:
V(t)=V0sin(ωt)
Substituting the values we calculated:
V(t)=311.13sin(100πt)
Conclusion
The instantaneous value of voltage as a function of time is:
V(t)=311.13sin(100πt)
---
The given RMS voltage (VRMS) is 220 V.
The peak voltage (V0) can be calculated using the relationship between RMS voltage and peak voltage:
V0=VRMS×√2
Substituting the given value:
V0=220V×√2≈220×1.414≈311.13V
The angular frequency (ω) is related to the frequency (f) by the equation:
ω=2πf
Given that the frequency (f) is 50 Hz:
ω=2π×50Hz=100πrad/s
The instantaneous voltage (V) as a function of time (t) can be expressed as:
V(t)=V0sin(ωt)
Substituting the values we calculated:
V(t)=311.13sin(100πt)
The instantaneous value of voltage as a function of time is:
V(t)=311.13sin(100πt)
Similar Questions
An AC source rated 220 V, 50 Hz is connected to a resistor. The time taken by the current to change from its maximum to the rms value is :
View SolutionAn inductor (L=200mH) is connected to an AC source of peak emf210V and frequency 50Hz. Calculate the peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View Solution
Knowledge Check
- Question 1 - Select One
The domestic power supply of 220 V, 50 Hz is connected to a resistor. What is the time taken by the alternating current flowing in the resistor, to change from its maximum value to turns value?
A5×10−3sB2.5×10−3SC10×10−3SD2.5×103S - Question 2 - Select One
120 V AC voltage is applied to 10 ohm resistance. The peak voltage across the resistor is
A120 VB120√2VC120√2VDnone of these - Question 3 - Select One
A 220V,50HzAC supply is connected across a resistor of 50kω. The current at time t second. Assuming that it is zero at t=0, is
A4.4sin(314t)mAB6.2sin(314t)mAC4.4sin(157t)mAD6.2sin(157t)mA
A 50 Ω resistor is connected in series to an inductor and a capacitor to an AC source 220 V , 50 Hz . Calculate the value of inductance and capacitance if voltages across resistor inductor and capacitor are 75 V , 210 V and 420 V respectively.
View SolutionA resistance of 40Ω is connected to an source of 220 v, 50 Hz. Find the (i) rms current (ii) maximum instantaneous current in resistor.
View SolutionThe electric mains in the house are marked 220 V, 50 Hz. Write down the equation for instantaneous voltage.
View SolutionFind the rms value of current if the peak value of an alternating voltage applied to a 20 ω resistance is 8 V . Also write the equation for instantaneous current if the voltange frequency is 60 Hz.
View SolutionA sinusoidal voltage of rms value 220 V is applied to a diode and a resistor R in the circuit shown in figure so that half wave rectification occurs. If the diode is ideal, what is the rms voltage across R1?
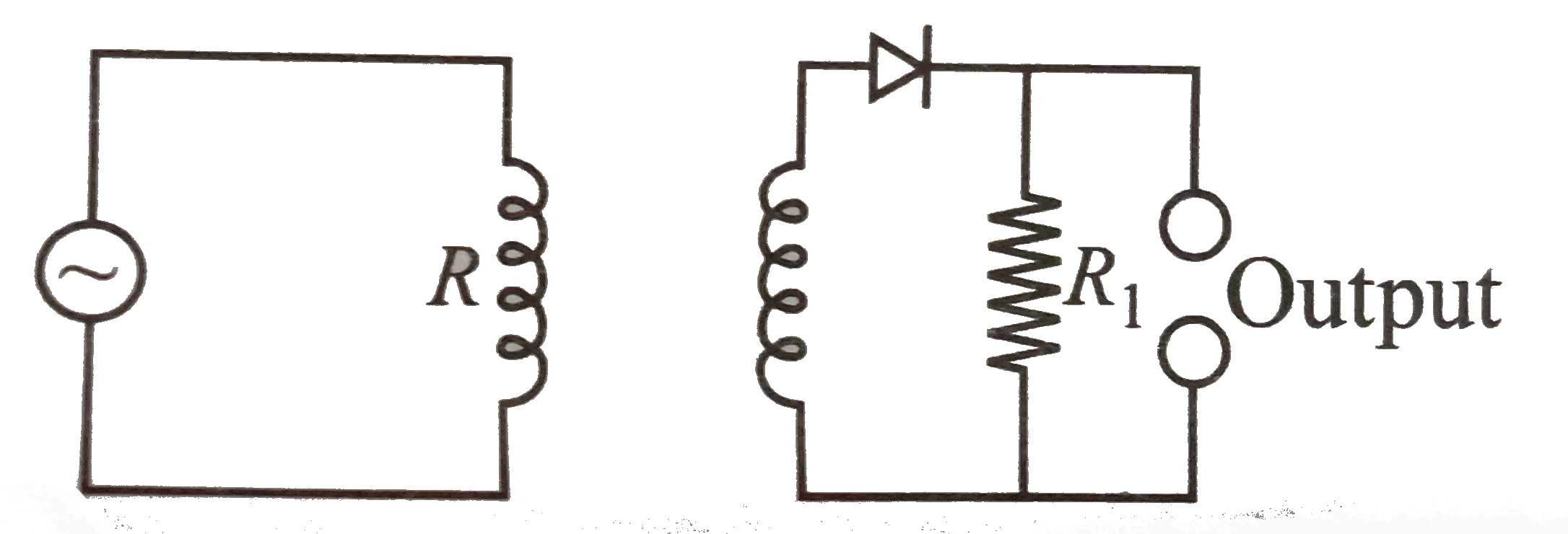 View Solution
View Solution

