2n identical cubical blocks are kept in a straight line on a horizontal smooth surface. The separation between any two consecutive blocks is same. The odd numbered blocks 1,3,5,.....(2n–1) are given velocity v to the right whereas blocks 2,4,6,......2n are given velocity v to the left. All collisions between blocks are perfectly elastic. Calculate the total number of collisions that will take place.

The correct Answer is:n(n+1)2
Step by step video, text & image solution for 2n identical cubical blocks are kept in a straight line on a horizontal smooth surface. The separation between any two consecutive blocks is same. The odd numbered blocks 1, 3, 5,.....(2n–1) are given velocity v to the right whereas blocks 2, 4, 6,......2n are given velocity v to the left. All collisions between blocks are perfectly elastic. Calculate the total number of collisions that will take place. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A large number of small identical blocks, each of mass m, are placed on a smooth horizontal surface with distance between two successive blocks being d. A constant force F is applied on the first block as shown in the figure
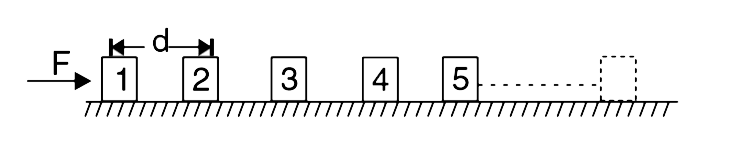
(a) If the collisions are elastic, plot the variation of speed of block 1 with time.
(b) Assuming the collisions to be perfectly inelastic, find the speed of the moving blocks after n collisions. To what value does this speed tend to if n is very large.
View SolutionInfinite blocks each of mass M are placed along a straight line with a distance d between each of them. At t = 0 the leftmost block is given a velocity V towards right. The coefficient of frication between any block and the surface is μ and all collisions are elastic. Let the total number of collisions be N then N is

View Solution
Knowledge Check
A set of n identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surfaces of any two adjacent blocks is L . The block at one end is given a speed v towards the next one at time 0 t . All collisions are completely inelastic, then
AThe last block starts moving at t=(n−1)LvBThe last block starts moving at t=n(n−1)L2vCthe centre of mass of the system will have a final speed vDThe centre of mass of the system will have a final speed vn.Two balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinity
The friction coefficient between the horizontal surface and blocks A and B are 115 and 215 respectively. The collision between the blocks is perfectly elastic. Find the separation (in meters) between the two blcoks when they come to rest.

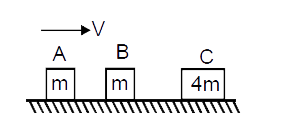
View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is
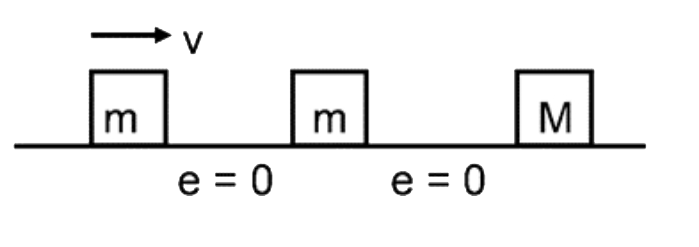
View SolutionThree blocks of masses m , m and M are kept on a frictionless floor as shown in the figure .The leftmost block is given velocity v towards the right . All the collision between the blocks are perfectly inelastic . The loss in kinetic energy after all the collision is 5/6th of initial kinetic energy. The ratio of M/m will be
View SolutionThree blocks are initially placed as shown in the figure. Block A has mass m and initial velocity v to the right. Block B with mass m and block C with mass 4 m are both initially at rest. Neglect friction. All collisions are elastic. The final velocity of block A is

View SolutionA block A of mass m is over a plank B of mass 2m. Plank B si placed over a smooth horizontal surface. The coefficient of friction between A and B is 12. Blocks A is given a velocity V0 towards right. Then
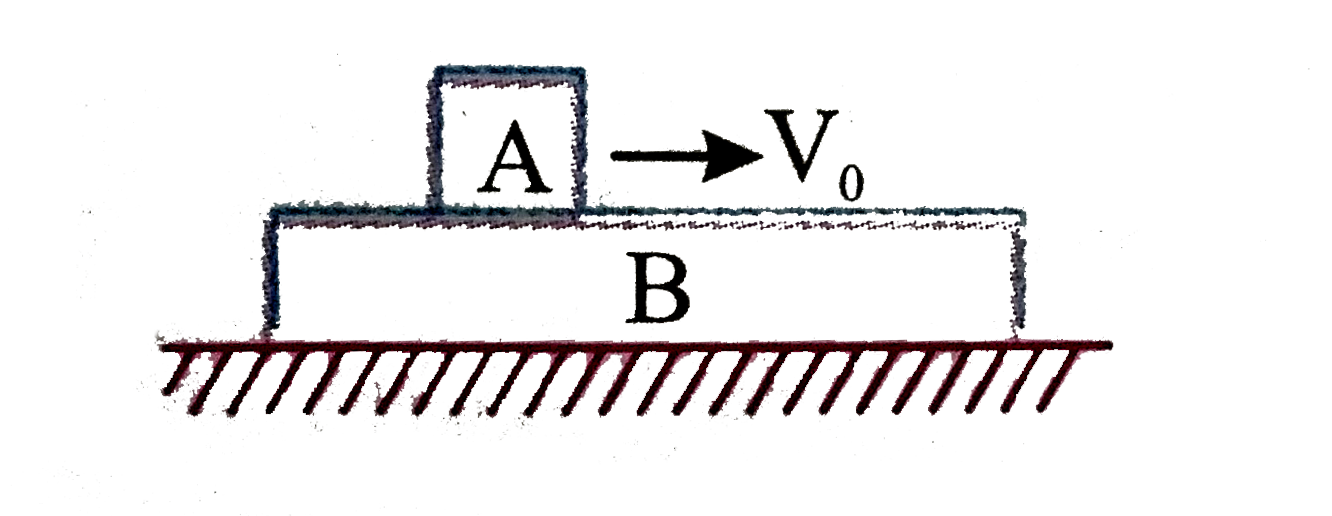
View Solution
