32 cells each of emf 3V are connected in series and kept in a not External the combination shown as emf 84V How many number of cells are connected reversely?
The correct Answer is:2
To solve the problem of how many cells are connected reversely in a series of 32 cells, each with an EMF of 3V, we can follow these steps:
Step 1: Calculate the total EMF if all cells are connected in the same polarity.
If all 32 cells are connected in the same polarity, the total EMF (E_total) can be calculated as:
Etotal=N×E
Where:
- N=32 (total number of cells)
- E=3V (EMF of each cell)
Substituting the values:
Etotal=32×3=96V
Step 2: Identify the actual total EMF given in the problem.
The problem states that the combination has an actual EMF of 84V.
Step 3: Determine the difference in EMF.
Now, we find the difference between the total EMF if all cells were connected in the same polarity and the actual EMF:
Difference=Etotal−Eactual=96V−84V=12V
Step 4: Relate the difference in EMF to the number of cells connected in reverse polarity.
When cells are connected in reverse polarity, their EMF effectively reduces the total EMF. Each cell connected in reverse polarity reduces the total EMF by twice its EMF (since it opposes the EMF of the other cells).
Let M be the number of cells connected in reverse polarity. The reduction in EMF due to these cells can be expressed as:
Reduction=2M×E
Where E=3V.
Setting this equal to the difference we calculated:
2M×3=12
Step 5: Solve for M.
Now, we can solve for M:
6M=12⟹M=126=2
Conclusion
Thus, the number of cells connected reversely is M=2.
---
If all 32 cells are connected in the same polarity, the total EMF (E_total) can be calculated as:
Etotal=N×E
Where:
- N=32 (total number of cells)
- E=3V (EMF of each cell)
Etotal=32×3=96V
The problem states that the combination has an actual EMF of 84V.
Now, we find the difference between the total EMF if all cells were connected in the same polarity and the actual EMF:
Difference=Etotal−Eactual=96V−84V=12V
When cells are connected in reverse polarity, their EMF effectively reduces the total EMF. Each cell connected in reverse polarity reduces the total EMF by twice its EMF (since it opposes the EMF of the other cells).
Reduction=2M×E
Where E=3V.
2M×3=12
Now, we can solve for M:
6M=12⟹M=126=2
Thus, the number of cells connected reversely is M=2.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)4videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-29videos
COMMUNICATION SYSTEMS
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Three identical cells of e.m.f. 1.5V are connected in parallel. The total e.m.f. of the combination is _____.
A1.5VB30VC4.5VD0.5V - Question 2 - Select One
Five dry cell each of e.m.f 1.5V are connected in parallel. The e.m.f of the combination is
A7.5 VB0.3 VC3VD1.5 V - Question 3 - Select One
Three identical cells of e.m.f. 1.5V are connected in parallel. The total e.m.f. of the combination is _____.
A1.5B4.5C0.5D3
n identical cells each of emf 6 V , connected in series with an external resistor of 5Ω, carry a current of 10A. If two cells are connected wrongly in series with the same external resistor, the current flowing through the cells will be 8A. Find the value of n and r the internal resistance of each cell.
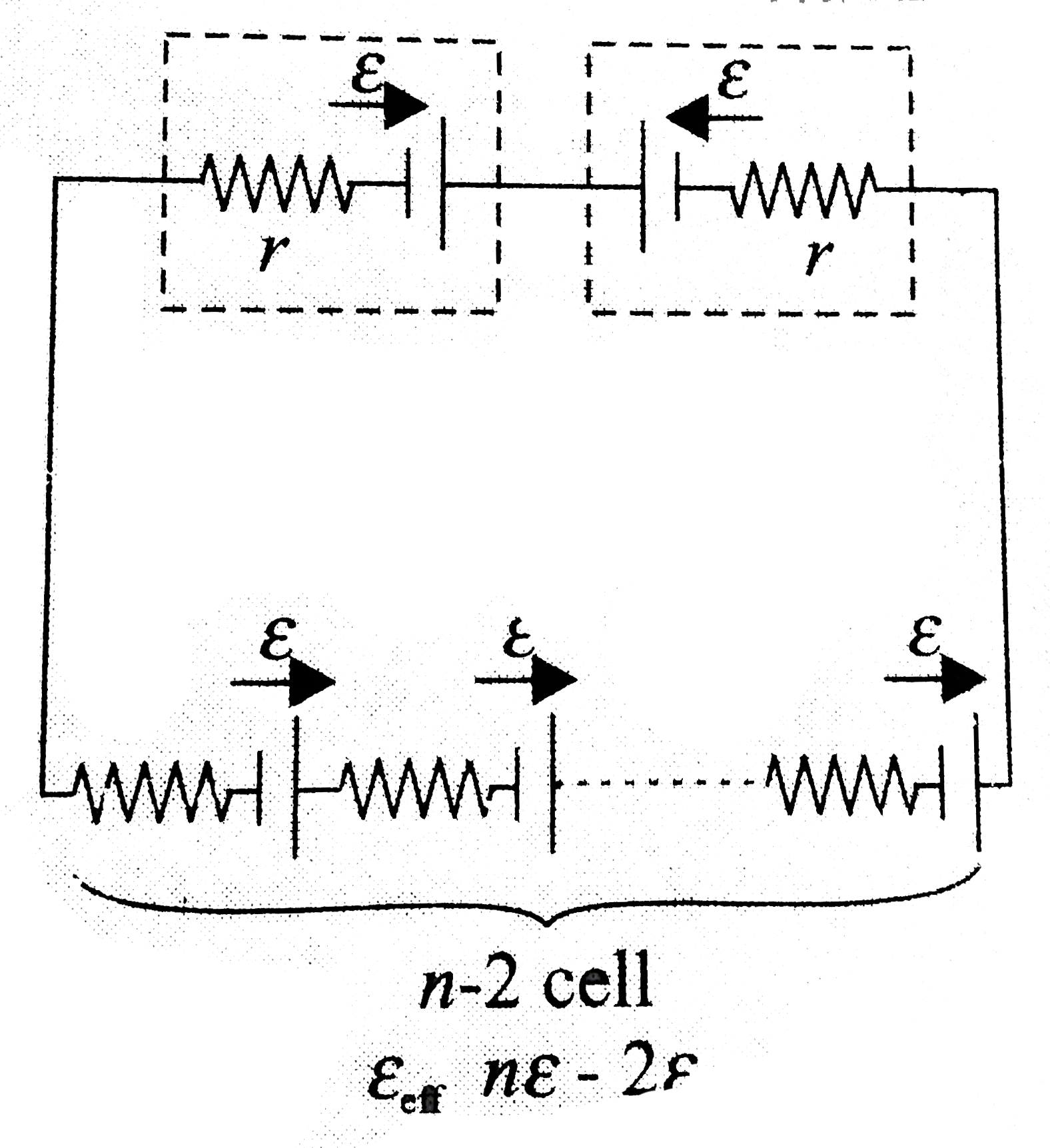 View Solution
View Solution(a) The emf of a cell is E and its intenal resistance is r. Its terminals are connected to a resistance R. The potential difference between the terminal is 12V if R=3Ω and 16V if R=8Ω. Find the values of E and r
(b) When an unknown resistance is connected across a series combination of two identical cells, each of 18V, current through the resistance is 4A. When it is connected across a parallel combination of the same cells, the current through it is 3A. Find the unknown resistance and internal resistance of each cell.
( c) p identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. One cell (X) is joined with reversed polarity. Find the potential difference across each cell except X and also across X.
(d) 12 cells each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ideal ammeter and two cells of same emf as of 12 cells. The current is 3A when the cells and the battery aid each other and 2A when the cells and battery oppose each other. How many cells in the battery are wrongly connected ?View SolutionA galvanometer together with an unkonwn resistance in series is connected across two identical cells, each of emf 1.5 V. When the cells are connected inseries, the galvanometer records a current of 1 A and when the cells are connected in parallel, the current =0.6 A. What is the internal resistance of each cell ?
View Solution12 cells of each emf 2 V are connected in series among them, if 3 cells are connected wrongly.Then the effective emf Of the combination is
View Solution12 cells of each emf 2 V are connected in series among them, if 3 cells are connected wrongly.Then the effective emf. Of the combination is
View Solution

