5 resistances R1,R2,R3,R4,R5 are joined as shown in the figure.

The values of R1,R2,R3andR4 are so adjusted that the current in the circuit does not change for any value of the resistance R5. This is possible for the following relation
A
R1+R2=R3+R4
B
R1R4=R2R3
C
R1R4=R3R2
D
1R1+1R3=1R2+1R4
Video Solution
Text Solution
The correct Answer is:C
This is balanced wheatstone's network.
∴ The relation is R1R2=R3R4orR1R4=R2R3
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
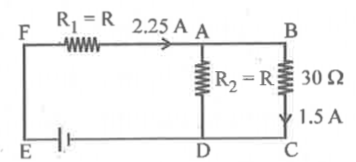
In the circuit shown in the given figure, the resistances R1andR2 are respectively
 A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30Ω
A14Ωand40ΩB40Ωand44ΩC40Ωand30ΩD14Ωand30ΩIn any triangle, the minimum value of r1r2r3/r3 is equal to
A1B9C27Dnone of theseTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>r1+r2BR>√r1r2Cr1<R<r2DR<r1
Find out the relation between R1,R2,R3andR4.so there is no that current in R.

View SolutionIn any triangle ABC, find the least value of r1+r2+r3r
View SolutionIn the situation shown, resistance R1,R2 and R3 are in the ratio 3:2:1 , then
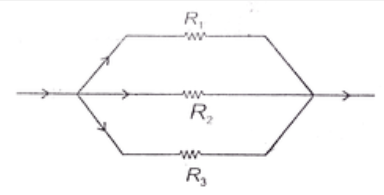
View SolutionIn the circuit shown in figure , R1=R2=R3=R. Match the following

View SolutionIn any triangle ABC, the least value of r1+r2+r3r is
View Solution