50g of oxygen at NTP is compressed adiabatically to a pressure of 5 atmosphere. The work done on the gas, if γ=1.4andR=8.31Jmol−1K−1 is
−5173J
1131J
−1364J
5673J
The correct Answer is:A
To solve the problem, we need to calculate the work done on 50g of oxygen gas during an adiabatic compression from NTP to a pressure of 5 atm. We will follow these steps:
Step 1: Calculate the number of moles of oxygen (n)
The molecular mass of oxygen (O₂) is 32 g/mol (16 g/mol for each oxygen atom).
n=massmolecular mass=50 g32 g/mol=1.5625 mol
Step 2: Determine the initial temperature (T₁)
At Normal Temperature and Pressure (NTP), the temperature is given as:
T1=273 K
Step 3: Use the adiabatic relation to find the final temperature (T₂)
The adiabatic relation between pressure and temperature is given by:
P1P2=(T1T2)γγ−1
Where:
- P1=1 atm (initial pressure at NTP)
- P2=5 atm (final pressure)
- γ=1.4
Substituting the values, we have:
15=(273T2)1.40.4
This simplifies to:
15=(273T2)3.5
Taking the reciprocal and raising both sides to the power of 13.5:
T2273=513.5
Calculating 513.5≈1.903:
T2=273×1.903≈519.2 K
Step 4: Calculate the work done (W)
The work done on the gas during adiabatic compression is given by:
W=nR(T2−T1)γ−1
Where:
- R=8.31 J/(mol K)
- T1=273 K
- T2≈519.2 K
Substituting the values:
W=1.5625×8.31×(519.2−273)0.4
Calculating the temperature difference:
T2−T1=519.2−273=246.2 K
Now substituting:
W=1.5625×8.31×246.20.4
Calculating further:
W=1.5625×8.31×615.5≈1.5625×5112.83≈7999.99 J
Since work done on the gas is considered negative during compression:
W≈−8000 J
Final Result
The work done on the gas during adiabatic compression is approximately −8000 J.
---
The molecular mass of oxygen (O₂) is 32 g/mol (16 g/mol for each oxygen atom).
At Normal Temperature and Pressure (NTP), the temperature is given as:
The adiabatic relation between pressure and temperature is given by:
- P1=1 atm (initial pressure at NTP)
- P2=5 atm (final pressure)
- γ=1.4
The work done on the gas during adiabatic compression is given by:
- R=8.31 J/(mol K)
- T1=273 K
- T2≈519.2 K
The work done on the gas during adiabatic compression is approximately −8000 J.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
1 litre of a gas at STP is expanded adiabatically to 3 litre. Find work done by the gas. Given γ = 1.40 and31.4=4.65
View Solution1 litre of a gas at STP is expanded adiabatically to 3 litre. Find work done by the gas. Given γ = 1.40 and31.4=4.65
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View SolutionThe volume of a given mass of gas at NTP is compressed adiabatically to 1/5th of its original volume. What is the new pressure ? γ=1.4.
View SolutionA vessel of capacity 3 litres contains 22g of CO2 and 28 g of nitrogen at 30∘C. Calculate the partial pressure and hence the total pressure exerted by the gas mixture. R = 8.31 J mol−1K−1.
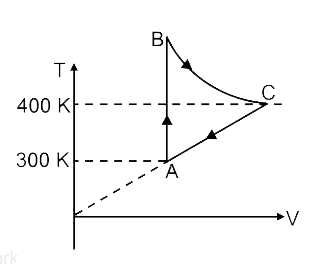
View Solution3 mole of an ideal gas is taken through the process shown. BC is adiabatic and the total work done in the cycle is 560 J. (γ=1.4,R=8.31Jm o1−1K−1 , take (4/3)0.4=1.125) Choose correct Options.
View SolutionFind the kinetic energy of 1 g of nitrogen gas at 77∘C. Given R=8.31 J mol−1K−1
View Solution10mol of an ideal gas confined to a volume of 10L is released into atmosphere at 300K where the pressure is 1bar. The work done by the gas is (R=0.083LbarK−1mol−1)
View SolutionFive moles of hydrogen (γ=7/5), initially at STP, is compressed adiabatically so that its temperature becomes 400∘C. The increase in the internal energy of the gas in kilojules is (R=8.30J/mol−K)
View SolutionOne litre of dry air STP undergoes through an adiabatic process and reaches to a final temperature of 89.6 °C, the work done by air is : [Take air to be an ideal gas and γair=1.4 use R=8.3Jmol−1K−1]
View Solution
