A 0.065 kg tennis ball moving to the right with a speed of 15 m/s is struck by a tennis racket, causing it to move to the left with a speed of 15 m/s. If the ball remains in contact with the racquet for 0.020 s, what is the magnitude of the average force experienced by the ball?
0N
98 N
160 N
240 N
The correct Answer is:B
To solve the problem of finding the magnitude of the average force experienced by the tennis ball, we can follow these steps:
Step 1: Identify the given values
- Mass of the tennis ball (m) = 0.065 kg
- Initial velocity (u) = 15 m/s (to the right)
- Final velocity (v) = -15 m/s (to the left, hence negative)
- Time of contact (Δt) = 0.020 s
Step 2: Calculate the initial momentum (p_initial)
The initial momentum (p_initial) can be calculated using the formula:
pinitial=m⋅u
Substituting the values:
pinitial=0.065kg⋅15m/s=0.975kg m/s
Step 3: Calculate the final momentum (p_final)
The final momentum (p_final) can be calculated using the formula:
pfinal=m⋅v
Substituting the values:
pfinal=0.065kg⋅(−15m/s)=−0.975kg m/s
Step 4: Calculate the change in momentum (Δp)
The change in momentum (Δp) is given by:
Δp=pfinal−pinitial
Substituting the values:
Δp=−0.975kg m/s−0.975kg m/s=−1.95kg m/s
Step 5: Calculate the average force (F_average)
The average force can be calculated using the formula:
Faverage=ΔpΔt
Substituting the values:
Faverage=−1.95kg m/s0.020s=−97.5N
Step 6: Determine the magnitude of the average force
Since we are interested in the magnitude of the average force, we take the absolute value:
|Faverage|=97.5N
Thus, the magnitude of the average force experienced by the ball is approximately 98 N.
- Mass of the tennis ball (m) = 0.065 kg
- Initial velocity (u) = 15 m/s (to the right)
- Final velocity (v) = -15 m/s (to the left, hence negative)
- Time of contact (Δt) = 0.020 s
The initial momentum (p_initial) can be calculated using the formula:
pinitial=m⋅u
Substituting the values:
pinitial=0.065kg⋅15m/s=0.975kg m/s
The final momentum (p_final) can be calculated using the formula:
pfinal=m⋅v
Substituting the values:
pfinal=0.065kg⋅(−15m/s)=−0.975kg m/s
The change in momentum (Δp) is given by:
Δp=pfinal−pinitial
Substituting the values:
Δp=−0.975kg m/s−0.975kg m/s=−1.95kg m/s
The average force can be calculated using the formula:
Faverage=ΔpΔt
Substituting the values:
Faverage=−1.95kg m/s0.020s=−97.5N
Since we are interested in the magnitude of the average force, we take the absolute value:
|Faverage|=97.5N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Linked Comprehension)6videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems46videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
The tennis ball may leave the racket of a top player on the serve with a speed of 65 m/s If mass of the ball is 0.06 kg and is in bontact with the racket for 0.03 sec, what the average force n the ball ?
View SolutionA golf player hits a golf ball of mass 100 g and imparts it a speed of 50 m/s. If golf stick remains in contact with the ball for 0.01 s, then the average force exerted by the golf stick on the ball.
View Solution
Knowledge Check
- Question 1 - Select One
A 0.5kg ball moving with a speed of 12m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle . If the ball is in contact with the wall for 0.25s, the average force acting on the wall is
 A48NB24NC12ND96N
A48NB24NC12ND96N - Question 2 - Select One
A 1 kg ball moving with a speed of 20 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed at the same angle. If the ball is in contact with the wall for 0.5 seconds, the average force acting on the wall is
A96 NB48 NC24 ND40 N - Question 3 - Select One
A ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
A100NB10NC1ND0.1N
A 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA 0.5 kg ball moving with a speed of 12 m/s strikes a hard wall at an angle of 30∘ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 s, the average force acting on the wall is :
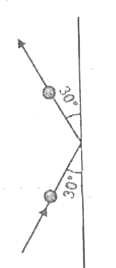 View Solution
View SolutionA ball weighing 50g hits a hard surface normally with a speed of 25m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.05s .The average force exerted by the surface on the ball is?
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
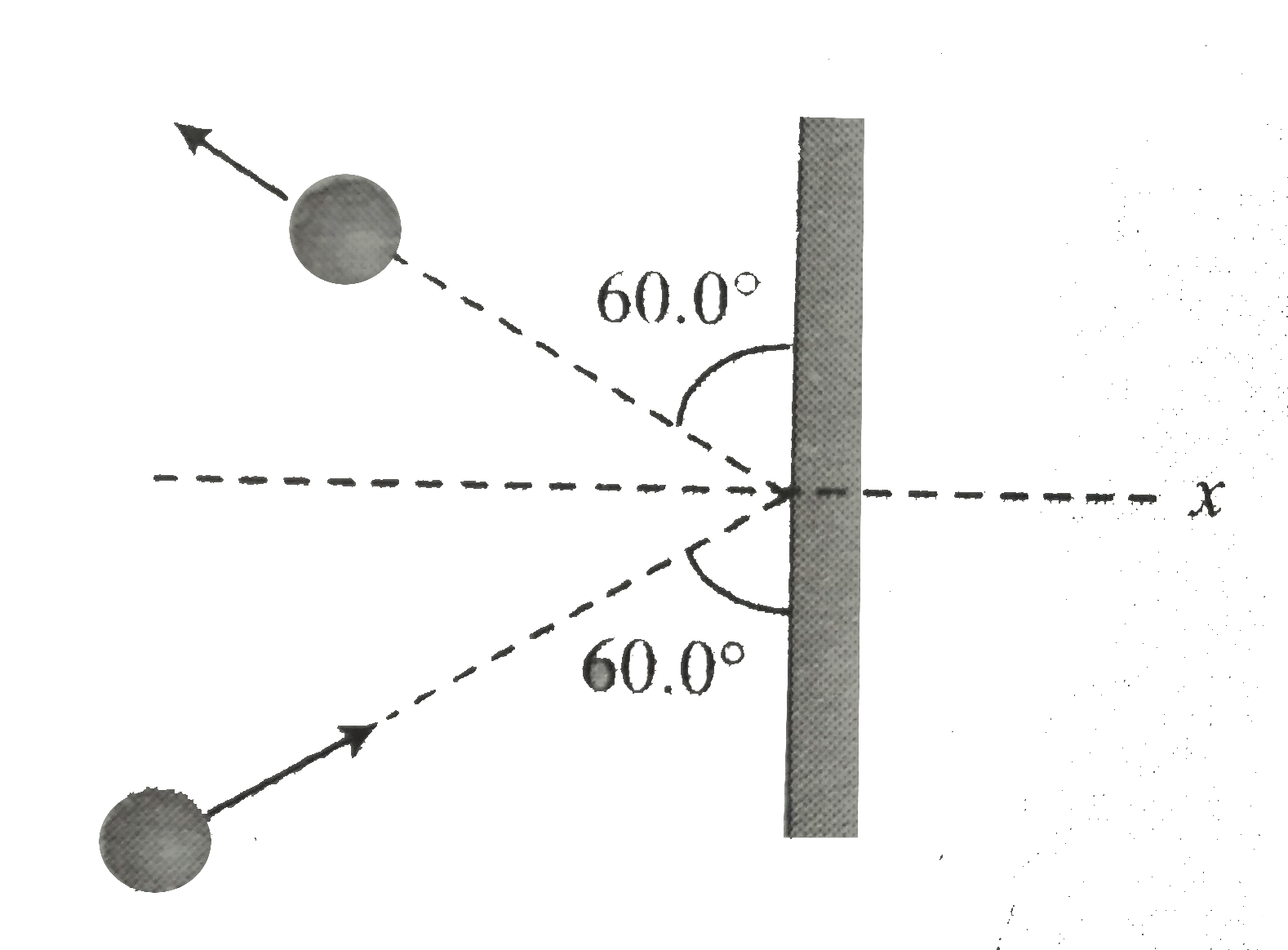 View Solution
View SolutionA ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
View Solution

