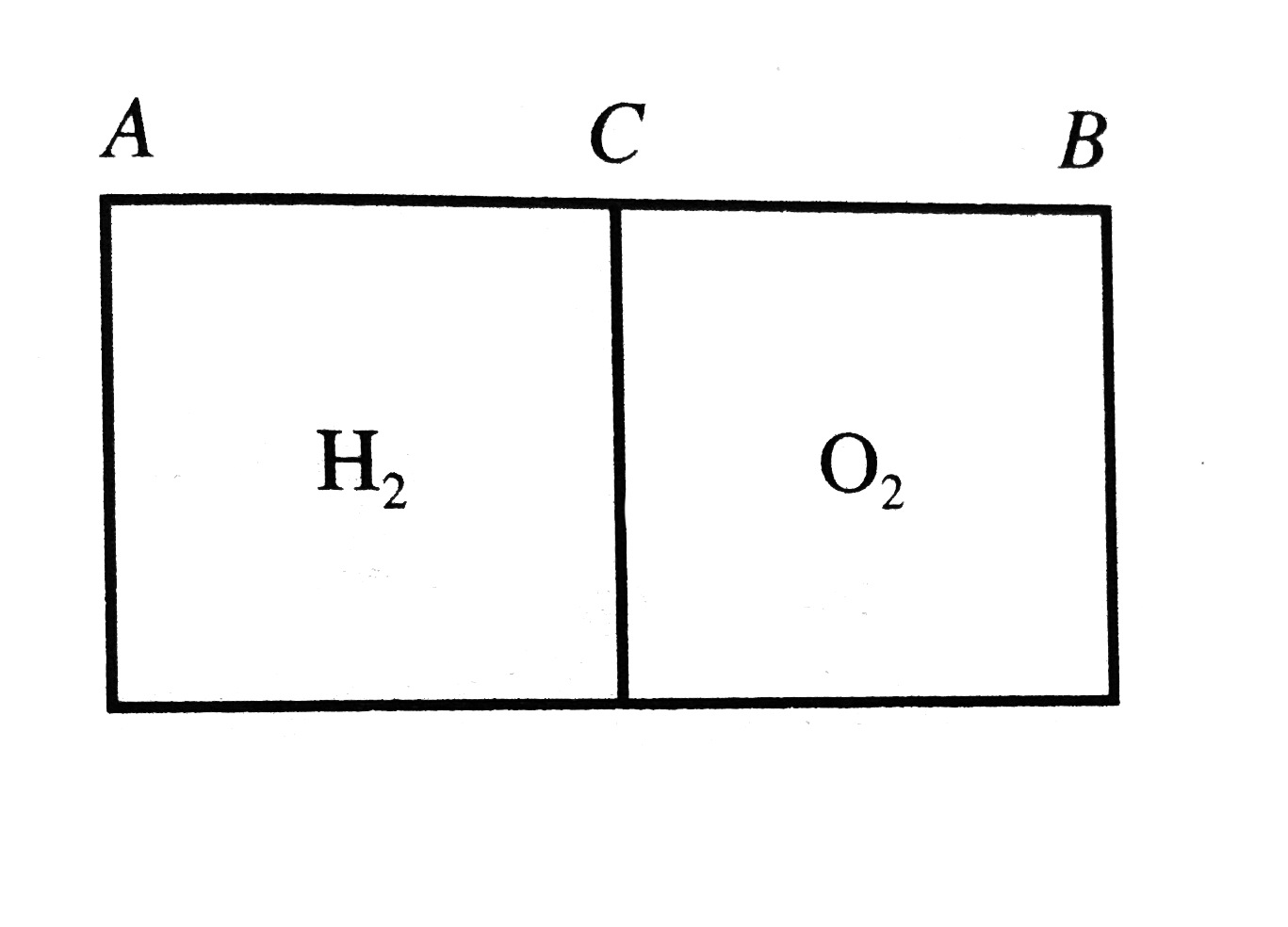
A 1 m long uniform cylindrical container is closed by two thin vibrating membranes A and B at its two ends [Fig . 4 . 15 ] . A third thin vibrating membrane C divides the container into two equal parts. The parts AC and BC are filled with haydrogen and oxygen gases, respectively . The membranes A and B are vibrated with the same frequency . Find out the minimum frequency of this vibration so that a node is formed at C . Given, velocities of sound in hydrogen and oxygen gases are 1100 and , respectively .
AB = 1 m , so AC = BC = 0 . 5 m = l (say) .
If the membranes A and B are vibrated, antinodes are produced at the points A and B . Given , a node is produced at the point c .
For an antinode at A and its adjacent node at C , the frequency is
Hz
Similarly, for the part BC
Hz
Now,
So, the frequency of the 3rd harmonic in AC matches exactly with that of the 11th harmonic in BC .
The minimum frequency Hz .

Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Higher order thinking skill (hots) questions
21 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Multiple choice questions (Based on standing wave)
5 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
- THERMOMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - THERMOMETRYEXERCISE - EXAMINATION ARCHIEVE - WBJEE
1 Videos
Similar Questions
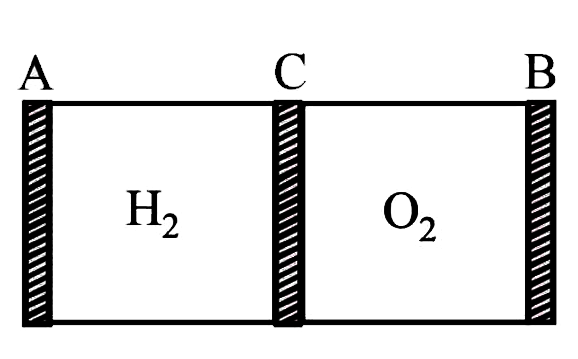
AB is a cylinder of length 1.0m fitted with a thin flexible diaphragm C at the middle and two others thin portions ACandBC contains hydrogen and oxygen gases , respectively . The diaphragms AandB are set into vibrations of same frequency . What is the minimum frequency of these vibrations for which the diaphragm C is a node ? Under the conditions of the experiment , the velocity of sound in hydrogen is 1100m/s and in oxygen is 300m/s.
View SolutionMitochondrial membranes divide its lumen into two ____ compartments.
View Solution
Knowledge Check
Seed coat is not thin, membranous in
AGramBMaizeCCoconutDGroundnutSeed coat is not thin, membranous in
AGroundnutBGramCMaizeDCoconut
Mitochondrial membranes divide its lumen into two ____ compartments.
View SolutionSeed coat is not thin, membranous in :
View SolutionAB is a ccylinder of length 1m fitted with a thin flexible diaphragn C at the middle and other thin flexible diaphragms A and B at the ends. The portions AC and BC contain hydrogen and oxygen gases respectively. The diaphragms A and B are set into vibrations of same frequency. what is the minimum frequency of these vibrations for which diaphragms C is a node? (Under the conditions of experiment vH2=1100m/s, v_(0_(2) = 300m//s).
View SolutionSeed coat is not thin, membranous in
View SolutionSeed coat is not thin, membranous in
View SolutionSeed coat is not thin, membranous in
View Solution
