A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
10ms−2
100ms−2
200ms−2
0.1ms−2
The correct Answer is:A
(a) We know that in spring SHM , the restoring force is proportional to displacement
i.e., F=−mω2y …(i)
F=−ky …(ii)
where ,k =force constant of the spring
m=10 kg ⇒ A=10 cm =0.1 m ⇒ k=1000Nm−1
Comparing the both equations , we get
ω2=km⇒ω=√km=√100010⇒10 rads−1
and acceleration in SHM.
amax=−ω2.y=−102×(0.1)=−10ms−2˜–10ms−2
Similar Questions

A 5-kg block rests on a smooth inclined plane of inclination 37∘ as shown in the diagram if the extension of spring is 6cm, find (a) the spring constant (b). If the block is pulled dow the incline 4 cm from its equilibrium position and released, find the initial acceleration of the block.
View SolutionA mass of 2 kg is attached to the spring constant 50Nm−1. The block is pulled to a distance of 5cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View Solution
Knowledge Check
A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
A10ms−2B100ms−2C200ms−2D0.1ms−2An oscillator consists of a block attached to a spring of spring constant K=300 N/m. At some time t the position (measured from its equilibrium position), velocity and acceleration of the block are
x=0.1m,v=−15m/s and a=−90m/s2. What is the ampliof motion and the mass of the block ?A0.3 m and 0.3 kgB0.4 m and 14kgC0.5 and 13kgD0.5m and 14kgTwo blocks of masses 3kg and 6kg rest on a horizontal smooth surface. The 3kg block is attached to a spring with a force constant k=900Nm−1 which is compressed 2m from beyond the equilibrium position. 3kg mass strikes the 6kgmass and two stick together-
 Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
Avelocity of the combined masses immediately arter the collision is 10ms−1Bvelocity of the conbined masses immediately after the collision is 5ms−1CAmplitude of the resulting oscillation is √2mDAmplitude of the resulting oscillation is √5/2m
A 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA block of mass one kg is fastened to a spring with a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Write the expression for its x(t) and v(t).
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
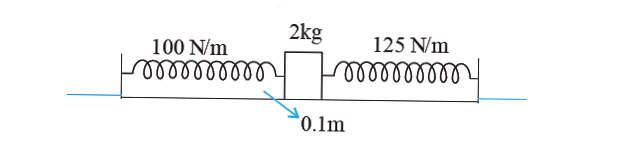
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionAn elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is

View Solution
