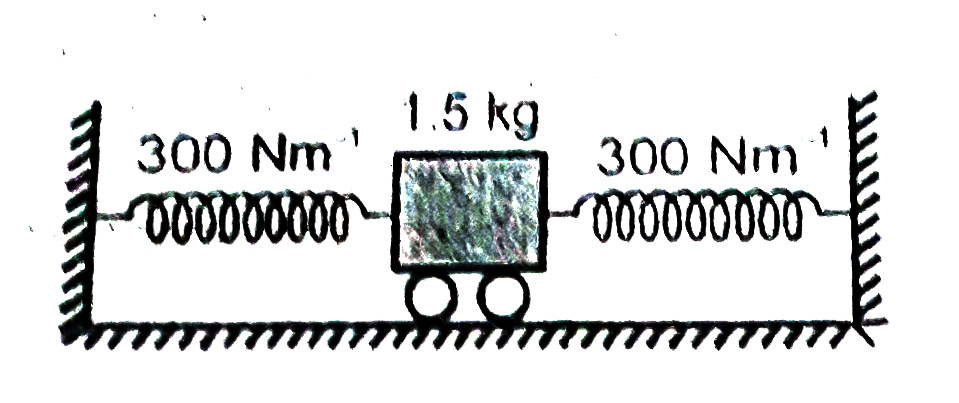A 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
10ms−2
100ms−2
200ms−2
0.1ms−2
The correct Answer is:A
To solve the problem step by step, we will follow the principles of simple harmonic motion (SHM) and use the given parameters.
Step 1: Identify the parameters
We are given:
- Mass of the block, m=10kg
- Spring constant, k=1000N/m
- Displacement from equilibrium (amplitude), A=10cm=0.1m
Step 2: Calculate the angular frequency (ω)
The angular frequency for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√1000N/m10kg=√100=10rad/s
Step 3: Calculate the maximum acceleration (Amax)
The maximum acceleration in simple harmonic motion is given by:
Amax=ω2A
Substituting the values we have:
Amax=(10rad/s)2×0.1m=100×0.1=10m/s2
Step 4: Conclusion
The maximum acceleration of the block is:
10m/s2
---
We are given:
- Mass of the block, m=10kg
- Spring constant, k=1000N/m
- Displacement from equilibrium (amplitude), A=10cm=0.1m
The angular frequency for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√1000N/m10kg=√100=10rad/s
The maximum acceleration in simple harmonic motion is given by:
Amax=ω2A
Substituting the values we have:
Amax=(10rad/s)2×0.1m=100×0.1=10m/s2
The maximum acceleration of the block is:
10m/s2
Similar Questions
Knowledge Check
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
A 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
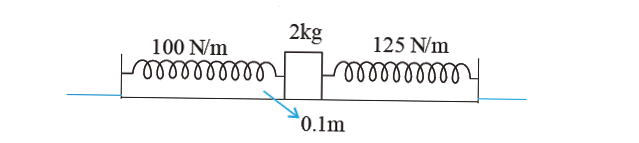
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0. Calculate the kinetic, potential and total energies of the block when it is 5cm away from the mean position.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution