A 100m long antenna is mounted on a 500m tall building. The complex can become a transmission tower of waves with λ
−400m
−25m
−150m
−2400m
The correct Answer is:A
To find the wavelength (λ) for the given antenna setup, we can follow these steps:
1. Identify Given Values:
- Length of the antenna (L) = 100 m
- Height of the building is not directly relevant for calculating the wavelength in this context.
2. Understand the Relationship:
- For a half-wave dipole antenna, the length of the antenna is approximately equal to half the wavelength (λ/2).
- For a quarter-wave antenna, the length of the antenna is approximately equal to one-fourth of the wavelength (λ/4).
3. Use the Formula:
- Since the problem implies that the antenna can be treated as a quarter-wave antenna, we can use the formula:
L=λ4
- Rearranging this gives:
λ=4L
4. Substitute the Values:
- Substitute the length of the antenna into the formula:
λ=4×100m
λ=400m
5. Conclusion:
- The wavelength (λ) for the given antenna setup is 400 meters.
Final Answer:
The wavelength (λ) is 400 meters.
---
- Length of the antenna (L) = 100 m
- Height of the building is not directly relevant for calculating the wavelength in this context.
- For a half-wave dipole antenna, the length of the antenna is approximately equal to half the wavelength (λ/2).
- For a quarter-wave antenna, the length of the antenna is approximately equal to one-fourth of the wavelength (λ/4).
- Since the problem implies that the antenna can be treated as a quarter-wave antenna, we can use the formula:
L=λ4
- Rearranging this gives:
λ=4L
- Substitute the length of the antenna into the formula:
λ=4×100m
λ=400m
- The wavelength (λ) for the given antenna setup is 400 meters.
The wavelength (λ) is 400 meters.
Topper's Solved these Questions
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - CORNER
15 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Introduction
2 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS
20 Videos
- ATOMS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A 100m long anteena is mounted on a 500m tall building. The complex can become a transmission tower for waves with λ.
View SolutionA 1.5m tall boy is standing at some distance from a 30m tall building. The angle of elevation from his eyes to the top of the building increases from 30∘ to 60∘ as he walks towards the building. Find the distance he walked towards the building.
View Solution
Knowledge Check
A TV transmitting antenna is 125 m tall. How much service area this transmitting antenna cover, if the receiving antenna is at the ground level? Radius of earth =6400km.
A3258km2B4180km2C2510km2D1525km2
How many 500 kHz waves can be on a 10 km transmission line simultaneously ?
View SolutionFrom a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of 20m high building are 45o and 60o respectively. Find the height of the transmission tower.
View SolutionFrom a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of 20m high building are 45o and 60o respectively. Find the height of the transmission tower.
View SolutionFrom a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
View SolutionFrom a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45∘and 60∘respectively. Find the height of the tower.
View SolutionThe height of a TV transmitting antenna is 20m. The telecast can cover a radius of
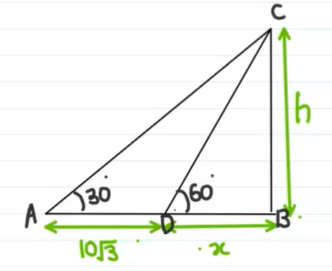
View SolutionAngle of elevation is the angle which line of sight makes with the horizontal. Angle of elevation of the top of a tall building is 30∘ from a place A and becomes 60∘ from another place B that is 10√3 m from A towards the building as shown in the figure. Height of the building is close to
View Solution
