A bullet pierces through a plate of mass and then comes to rest inside a second plate of mass as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between and . Neglect any loss of material of the plates due to the action of bullet.

The correct Answer is:B
Apply conservation of momentum after piercing :
………i
After it enters into , finally bullet also moves with velocity , so
……ii
From i and ii, we get
..........iii
Required percentage loss
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
04:51View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.03:09View SolutionTwo identical smooth balls are projected from points O and A on the horizontal ground with same speed of projection. The angle of projection in each case is 30∘.The distance between O and A is 100m. The balls collide in mid-air and return to their respective points of projection. If the coefficient of restitution is 0.7, find the speed of projection of either ball (in m/s) correct to nearest integer. (Take g=10ms−2 and √3=1.7)
 03:29View Solution
03:29View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.508:08View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
04:05View SolutionA 20 gm bullet pierces through a plate of mass m_(1) = 1 kg and then comes to rest inside a second plate of mass M_(2) = 2.98 kg as shown , it is found that the two plates initily atrest , now move with equal velocity . Find the percentage loss in the initial velocity of the bullet when it is between M and M_(2) neglet any loss of material of the pletes due to the action of the bullet
06:51View SolutionThree blocks m_(1), m_(2) , and m_(3) are arranged as shown in fig. if m_(2)=5 kg and m_(3)=8kg , at what value of m_(1) will 8kg mass be at rest?
View SolutionTwo wooden plank of mass M_(1)= 1 kg, M_(2) = 2.98 kg smooth surface. A bullet of mass m = 20 gm strikes the block M_(1) and pierces through it, then strikes the plank B and sticks to its. Consequently both the planks move with equal velocities. Find the percentage change in speed of the bullet when it escapes from the first block.
03:58View SolutionA 20g bullet pierces through a plate of mass M1=1kg and then comes to rest inside a second plate of mass M2=2.98kg as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1 and M2. Neglect any loss of material of the plates due to the action of bullet.
 02:37View Solution
02:37View SolutionA body of mass m_(1) collides elastically with another body of mass m_(2) at rest. If the velocity of m_(1) after collision is (2)/(3) times its initial velocity, the ratio of their masses is :
06:39View SolutionA m=20gm bullet pierces through a plate of mass M_(1) = 1kg and then comes to rest inside a second plate of mass M_(2) = 2.98 kg as shown in figure. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M_(1) "and"M_(2) . Neglect any loss of material of the plates, due to the action ofthe bullet.
05:57View SolutionIn the Fig 7.89 shown , m_(2) = 2.5 kg , h = 1.5 m , the system is released from rest at t = 0 and the mass m_(2) strikes ground at t = 0.82 s . The system is placed in its initial position and a 1.2 kg mass is placed on top of the block of mass m_(1) . Released from rest , the mass m_(2) now strikes the ground 1.3 s later . Determine the mass m_(1) and the coefficient of kinetic friction between m_(1) and the shelf .
02:25View SolutionA 20 g bullet pierces through a plate of mass M_(1)=1kg and then comes to rest inside a second plate of mass M_(2)=2.98 kg as shown in the figure. It is found that the two plates, initially at rest, now move with equal velocities, Find the percentage loss in the initial velocity of the bullet when it is between M_(1)and M_(2) . Neglect any loss of material of the plates due to the action of bullet
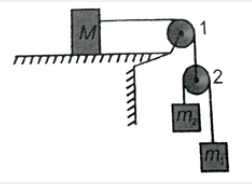
04:45View SolutionIn the arrangment as shown below m1=1kg,m2=2kg . Pulleys are massless and strings are light . For what value of M the mass m1 moves with constant velocity . ( Neglect Friction)
 04:26View Solution
04:26View SolutionIf a body of mass m_(1) moving with velocity v_(1) collides inelastically with another mass m_(2) at rest then give the expression for loss in the K.E. of the system.
View Solution

