A 200 mH (pure) inductor and a 5uF (pure) capacitor are connected, one by one, across a sinusoidal a.c. voltage source V= 70.7 sin (1000 t) volts. Obtain the expression for the current in each case.
Here L = 200 mH = 0.2 H, C=5μF×10−6F and V = 70.7 sin(1000 t) means that ω=1000s−1
For inductive cirucit Im=VmXL=VmLω=70.70.2×1000=0.354A
So expression for current will be, IL=Imsin(ωt−π2)=0.354sin(1000t−π2)A
For capacitive circuit, Im=VmXL=Vm.C.ω=70.7×5×10−6×1000=0.354A
∴ Expression for current will be, Ic=Imsin(ωt+π2)=0.354sin(1000t+π2)A
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - LONG ANSWER QUESTIONS -I26videos
ALTERNATING CURRENT
- BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - LONG ANSWER QUESTIONS -II12videos
ALTERNATING CURRENT
- BOOK - U-LIKE SERIESCHAPTER - ALTERNATING CURRENT EXERCISE - VERY SHORT ANSWER QUESTIONS28videos
ALTERNATING CURRENT
- BOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SELF ASSESSMENT TEST (SECTION C)2videos
ATOMS
Similar Questions
A 200 mH (pure) inductor, and a 5μF (pure) capacitor , are connected , one by across a sinusoidal ac voltage source V=[70.7sin(1000t)] voltage. Obtain the expressions for the current in each case.
View SolutionA 200 Mh (pure) inductor, and a 5μF (pure) capacitor , are connected , one by across a singusoidal ac voltage source V=[70.7sin(1000t)] voltage. Obtain the experiessions for the current in each case.
View Solution
Knowledge Check
- Question 1 - Select One
In ac circuit contains a pure capacitor, across which an ac emf
e=100sin(1000t), volt
is applied. If the peak value of the current is 200 mA, then the value of the capacitor isA2μB20μFC5μFD500μF - Question 2 - Select One
An inductor 20mH , a capacitor 50μF and a resistor 40Ω connected in series across a source of emf V=10sin340t. The power loss in A.C. circuit is
A0.51 WB0.67WC0.76 WD0.89 W - Question 3 - Select One
A sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. the current through the coil is
A10 cos (500t).B−10 cos (500t).C10 sin (500t)D−10 sin (500t)
An a.c. voltage V=Vm sin ot is applied across an inductor L. Obtain an expression for current I.
View SolutionA pure inductor and a pure resistor are connected in series and an ac supply is connected across this combination. Ideal ac volt meters v1 and v2 show 120 volt and 160 volt respectively . What is the phase difference between V1 and V2.
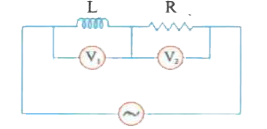 View Solution
View SolutionA pure inductor and a pure resistor are connected in series and an ac supply is connected across this combination. Ideal ac volt meters v1 and v2 show 120 volt and 160 volt respectively . What is the phase difference between V1 and V2.
 View Solution
View SolutionA 50 mH inductor is connected across a power supply of emf 130 sin (314 t) volts. Calculate the resistance of the inductor if maximum current in the circuit is 8 A.
View SolutionA 50 μF capacitor is connected to an ac source V = 220 sin50t where V is in volt and t is in second. The rms current is
View Solution
