A 3.00 kg object is released from rest while fully sub merged in a liquid. The liquid displaced by the submerged object has a mass of 5.00 kg. How far and in what direction does the object move in 0.200 s, assuming that it moves freely and that the drag force on it from the liquid is negligible?
To solve the problem step by step, we need to analyze the forces acting on the object and apply the equations of motion.
Step 1: Identify the forces acting on the object
The object has two main forces acting on it:
1. The weight of the object (downward force).
2. The buoyant force (upward force) due to the liquid displaced.
Step 2: Calculate the weight of the object
The weight W of the object can be calculated using the formula:
W=m⋅g
where:
- m=3.00kg (mass of the object)
- g=9.81m/s2 (acceleration due to gravity)
Thus, the weight of the object is:
W=3.00kg⋅9.81m/s2=29.43N
Step 3: Calculate the buoyant force
The buoyant force Fb can be calculated using the weight of the liquid displaced:
Fb=mass of liquid⋅g=5.00kg⋅9.81m/s2=49.05N
Step 4: Calculate the net force acting on the object
The net force Fnet acting on the object is the difference between the buoyant force and the weight of the object:
Fnet=Fb−W=49.05N−29.43N=19.62N
Step 5: Calculate the acceleration of the object
Using Newton's second law, F=m⋅a, we can find the acceleration a of the object:
a=Fnetm=19.62N3.00kg=6.54m/s2
Step 6: Calculate the distance moved in 0.200 seconds
Using the second equation of motion:
s=ut+12at2
where:
- u=0 (initial velocity since the object is released from rest)
- t=0.200s
- a=6.54m/s2
Substituting the values:
s=0+12⋅6.54m/s2⋅(0.200s)2
s=12⋅6.54⋅0.04=0.131m
Conclusion
The object moves 0.131 meters upward in 0.200 seconds.
---
The object has two main forces acting on it:
1. The weight of the object (downward force).
2. The buoyant force (upward force) due to the liquid displaced.
The weight W of the object can be calculated using the formula:
W=m⋅g
where:
- m=3.00kg (mass of the object)
- g=9.81m/s2 (acceleration due to gravity)
W=3.00kg⋅9.81m/s2=29.43N
The buoyant force Fb can be calculated using the weight of the liquid displaced:
Fb=mass of liquid⋅g=5.00kg⋅9.81m/s2=49.05N
The net force Fnet acting on the object is the difference between the buoyant force and the weight of the object:
Fnet=Fb−W=49.05N−29.43N=19.62N
Using Newton's second law, F=m⋅a, we can find the acceleration a of the object:
a=Fnetm=19.62N3.00kg=6.54m/s2
Using the second equation of motion:
s=ut+12at2
where:
- u=0 (initial velocity since the object is released from rest)
- t=0.200s
- a=6.54m/s2
s=0+12⋅6.54m/s2⋅(0.200s)2
s=12⋅6.54⋅0.04=0.131m
The object moves 0.131 meters upward in 0.200 seconds.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)48videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )10videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - CHECKPOINT8videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
A small solid ball is released from rest while fully sub merged in a liquid and then its kinetic energy is measured when it has moved 2.0 cm in the liquid. Figure 14.46 gives the results after many liquids are used: The kinetic energy K is plotted versus the liquid density ρliq and Ks = 2.4 J sets the scale on the vertical axis. What are (a) the density and (b) the volume of the ball?
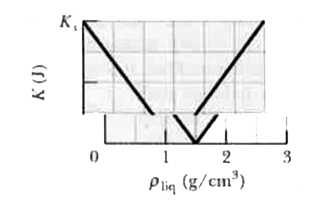 View Solution
View SolutionAn object of mass 200 kg is accelerated uniformly from a velocity of 4ms−1to8ms−1 in 10 s . Find the magnitude of the force exerted on the object
View Solution
Knowledge Check
- Question 1 - Select One
When a constant force acts on an object with a mass of 8 kg for a duration of 3 s, it increases the object's velocity from 4 ms−1 to 6 ms−1. What is the magnitude of the applied force?
AA) 5.33 NBB) 4.33 NCC) 6.33 NDD) 3.33 N - Question 2 - Select One
When a constant force acts on an object with a mass of 7 kg for a duration of 3 s , it increases the object's velocity from 3ms−1 to 8ms−1 . What is the magnitude of the applied force ?
A10.66 NB11.66 NC13.66 ND12.66 N - Question 3 - Select One
When a constant force acts on an object with a mass of 8 kg for a duration of 3 s, it increases the object's velocity from 6 4 ms−1 to 6 ms−1. What is the magnitude of the applied force?
A5.33 NB4.33 NC6.33 ND3.33 N
Two objects of equal volume V=1m3 and different densities d1=500kg/m3 and d2=1000kg/m3 are gluod to each other so that their contact surface is flat and has an area A=0.1m2 When the objects are submerged in a certain liquid they float in stable equilibrium the contact surface being parallel to the surface of the liquid (see the diagram) How deep (H in meters) can the contact surface be in the liquid so that the objects are not torn apart? The maximum force that the glue can with stand is F=250 N (Neglect atmospheric pressure)
 View Solution
View SolutionIn Fig. , a rectangular block floats in a liquid . A block of mass m = 0.500 kg and density ρ=700kg/m3 floats face down in a liquid of density ρf=1200kg/m3 . What are the magnitude of the buoyant force on the block from the liquid , the weight of the liquid displaced by the block (liquid that would be in the space now occupied by the block ) , and the mass of that displaced liquid ? What fraction of the block's volume is submerged ? What fraction of its height is submerged ?
 View Solution
View SolutionA space ship at rest on a launching pad has a mass of 1.00×105 kg. How much will its energy have increased when the ship is moving at 0.600c?
View SolutionAn object of mass 5 kg is acted upon by a force that varies with position of the object as shown. If the object starts out from rest at a point x=0. What is its speed at x=50 m.
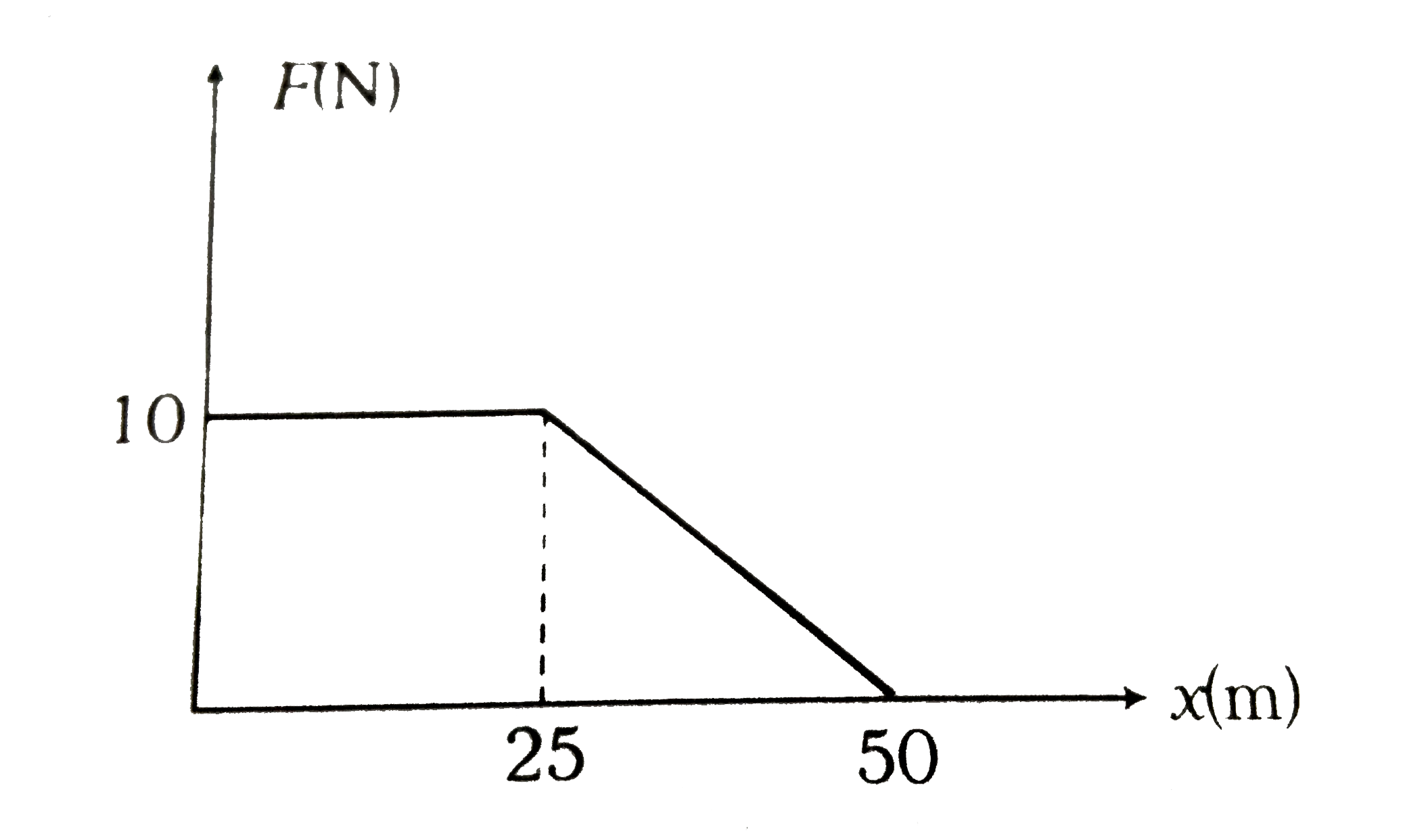 View Solution
View SolutionAn object of mass 5 kg is sliding on a smooth frictionless horizontal surface with a constant velocity of 10 m/s. the force required to keep the object moving with the same velocity is
View Solution

