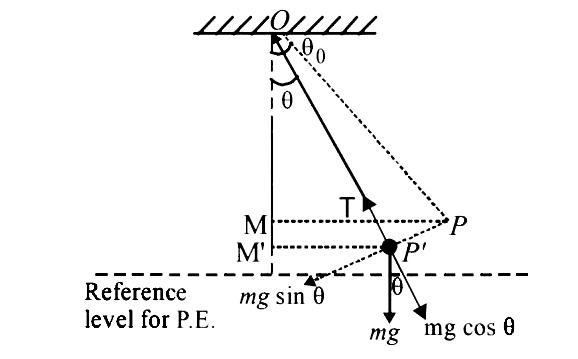
A 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude θ0. What is the tension in the rope when it makes en angle θ with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
The correct Answer is:A, B, C
T−mgcosθ=mv2l
∴T=mv2l+mgcosθ….(i)
In ΔOPM,cosθ0=OMi
⇒OM=Icosθ0
in ΔOP'M',cosθ=OMi
⇒OM=Icosθ
OM−OM=I(cosθ−cosθ0)
Loss in potential energy = Gain i kinetic energy
⇒mgl(cosθ−cosθ0)=12mv2
⇒v2=2gl(cosθ−cosθ0)
From (i) and (ii)
T=ml×2gl(cosθ−cosθ0)+mgcosθ
∴T=3mgcosθ−2mgcosθ0
⇒T=mg(3cosθ−2cosθ0)
From equation (i) it is clear that the tension is maximum
when cos theta = 1i.e., theta = 0^@<br>:. T = mg<br>Hence,T_(max) = (mv^2)/(l) + mg ....(iii)<br>Fromeqn.(ii)
v2=2gl(1−cosθ0)..(iv)
From (iii) and (iv)
Tmax=ml[2gl(1−cosθ0)]+mg
∴Tmax3mg−2mgcosθ0
80=3×40−2×40cosθ0
⇒80cosθ0=40⇒cosθ0=12⇒θ0=30∘.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A 40-kg mass hanging at the end of a rope of length l. Oscillates in a vertical plane with an angular of θ0. What is the tension in the rope when it makes an angle θ with the vertial ? If the breaking strength of the rope is 80 kg, what is the maximum angular amplitude with which the mass can oscillate without the rope breaking ?
View SolutionA boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View Solution
Knowledge Check
An object of mass 5 kg is attached to the end ofa rope. If the rope is pulled upward with an acceleration 0.30ms−2, what is the tension in the rope?
A30.5 NB40.5 NC50.5 ND60.5 NA simple pendulum of length 'l' carries a bob of mass 'm'. If the breaking strength of the string is 3mg, the maximum angular amplitude from the vertical can be
A0∘B30∘C60∘D90∘A mass of 10kg is suspended by a rope of length 2.8m from a ceiling. A force of 98N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
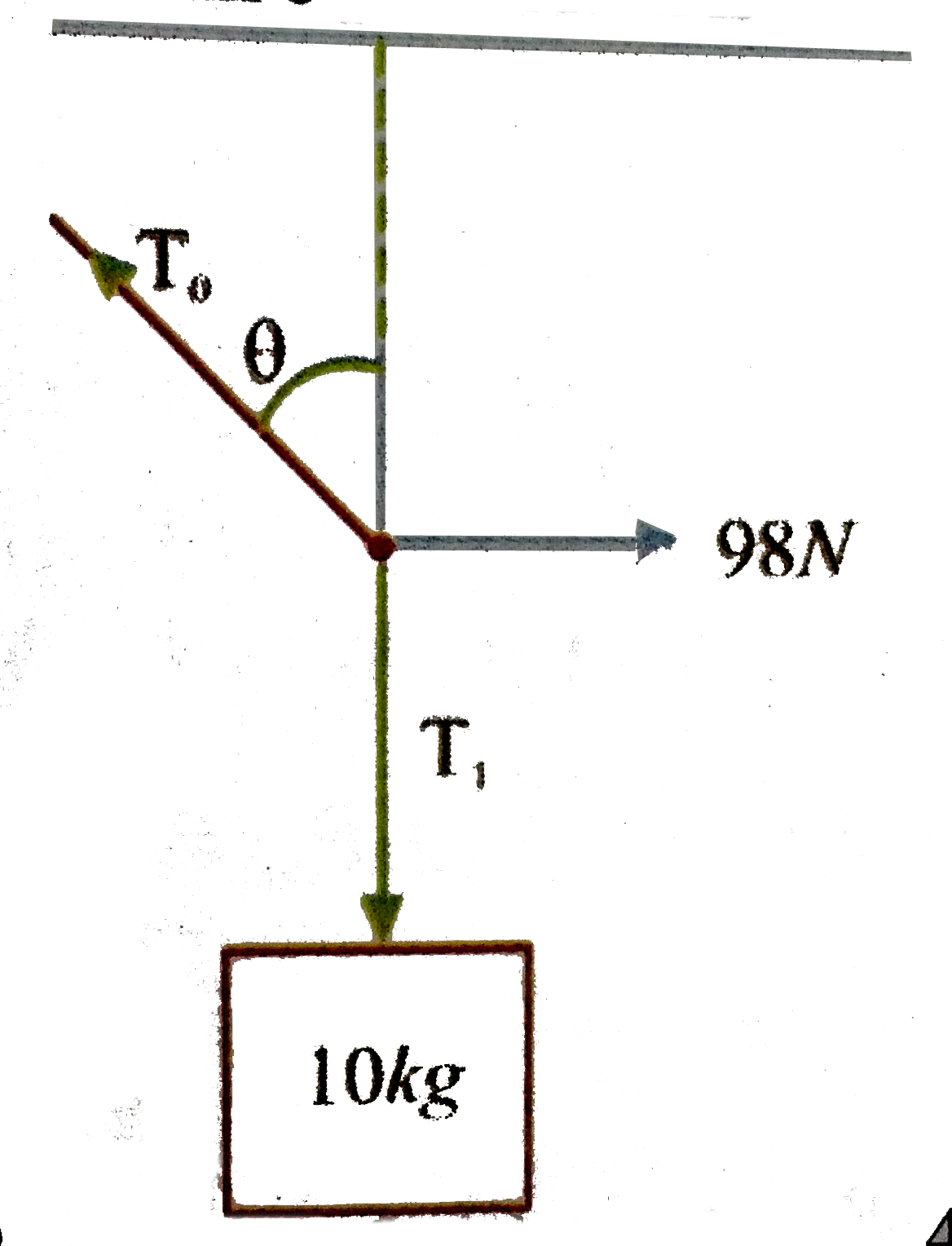 .A30∘B60∘C45∘D90∘
.A30∘B60∘C45∘D90∘
A ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle θ with vertical given by sinθ=r/2. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View SolutionA girl of mass 40 kg sits in a swing formed by a rope of 6 m length. A person pulls the swing to a side so that the rope makies an angle of 60∘ with the vertical. What is the gain in potential energy of the girl ?
View SolutionA mass of 10 kg is suspended by a rope of length 2.8m from a ceiling. A force of 98 N is applied at the midpoint of the rope as shown in figure. The angle which the rope makes with the vertical in equilibrium is
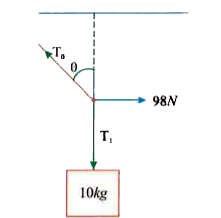
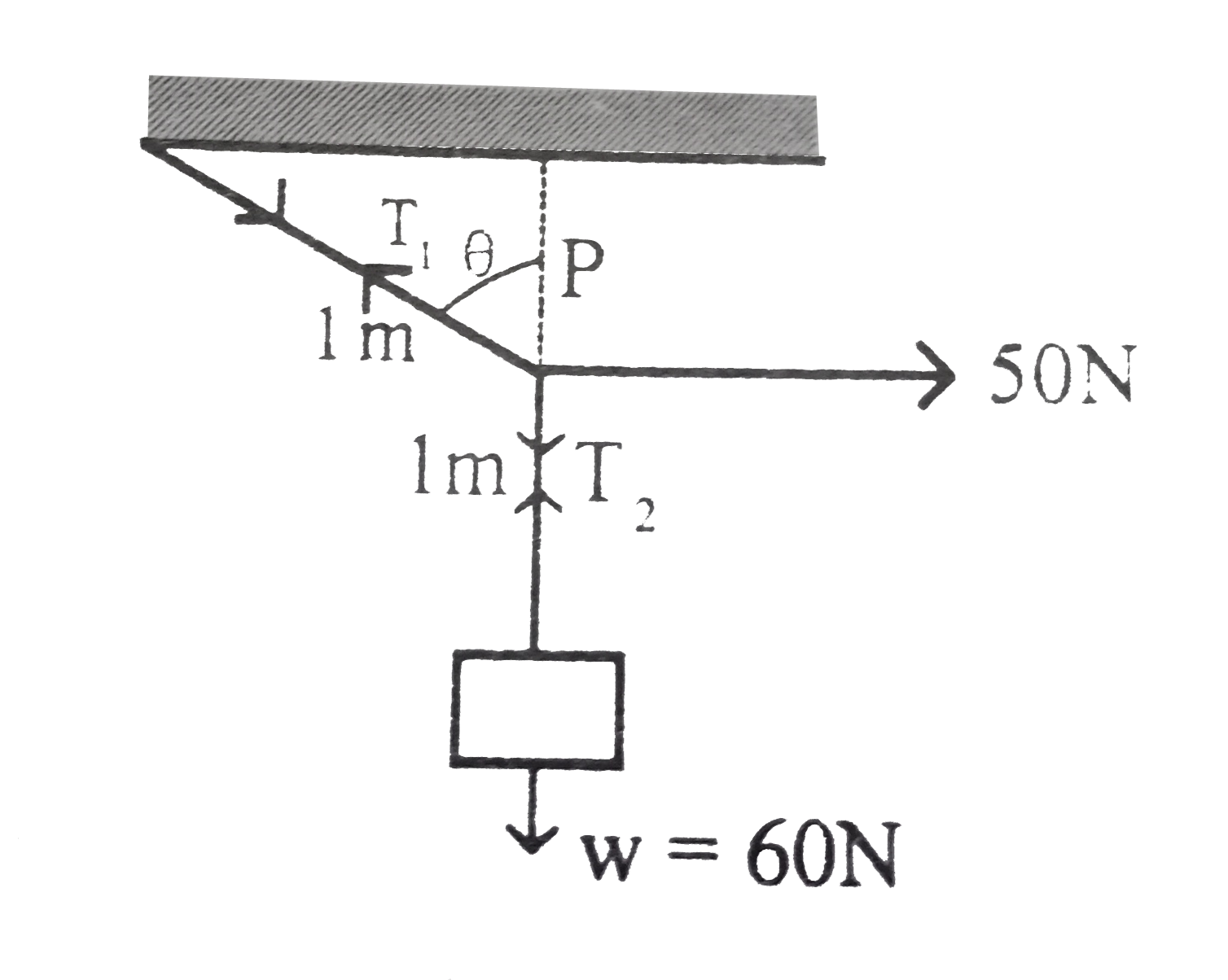
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
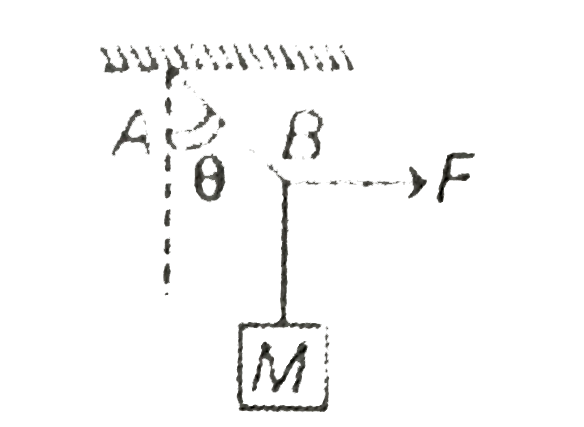
View Solution
