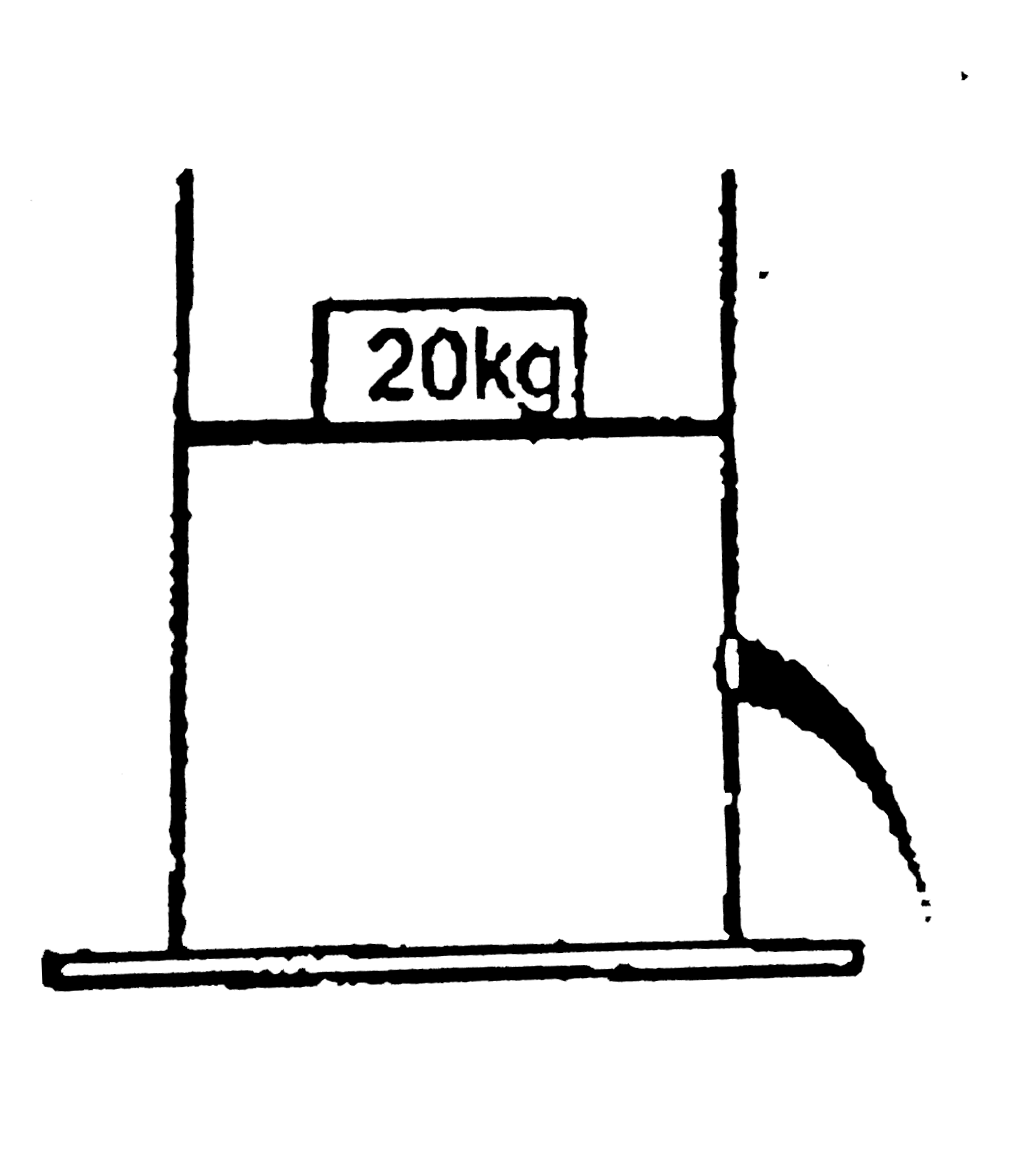
A area of cross section of a large tank is $0.5 m^{2}$ . It has an opening near the bottom having area of cross section $1 c m^{2}$ . A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take $g = 10 m s^{- 2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem step-by-step, we will use the principles of fluid mechanics, particularly Bernoulli's equation.
Step 1: Identify the given data
- Area of cross-section of the tank, $A_{t} = 0.5 m^{2}$
- Area of the opening, $A_{o} = 1 c m^{2} = 1 \times 10^{- 4} m^{2}$
- Load on the water, $m = 20 k g$
- Height of water level, $h = 50 c m = 0.5 m$
- Acceleration due to gravity, $g = 10 m / s^{2}$
Step 2: Calculate the pressure at point A (top of the water)
The pressure at point A consists of atmospheric pressure and the pressure due to the load on the water.
1. Calculate the force due to the load:
$F = m \cdot g = 20 k g \cdot 10 m / s^{2} = 200 N$
2. Calculate the pressure due to the load:
$P_{l o a d} = \frac{F}{A_{t}} = \frac{200 N}{0.5 m^{2}} = 400 P a$
3. The total pressure at point A (considering atmospheric pressure $P_{0}$ ):
$P_{A} = P_{0} + P_{l o a d} = P_{0} + 400 P a$
Step 3: Calculate the pressure at point B (opening)
At point B, the pressure is atmospheric pressure $P_{0}$ since it is exposed to the atmosphere.
Step 4: Apply Bernoulli's equation
Using Bernoulli's equation between points A and B:
$P_{A} + ρ g h + \frac{1}{2} ρ v_{A}^{2} = P_{B} + \frac{1}{2} ρ v_{B}^{2}$
Assuming $v_{A}$ (velocity at point A) is negligible, we can simplify this to:
$P_{A} + ρ g h = P_{B} + \frac{1}{2} ρ v_{B}^{2}$
Step 5: Substitute known values
1. Substitute $P_{A}$ and $P_{B}$ :
$(P_{0} + 400) + ρ g h = P_{0} + \frac{1}{2} ρ v_{B}^{2}$
2. Cancel $P_{0}$ :
$400 + ρ g h = \frac{1}{2} ρ v_{B}^{2}$
3. Substitute $ρ = 1000 k g / m^{3}$ , $g = 10 m / s^{2}$ , and $h = 0.5 m$ :
$400 + 1000 \cdot 10 \cdot 0.5 = \frac{1}{2} \cdot 1000 \cdot v_{B}^{2}$
$400 + 5000 = 500 \cdot v_{B}^{2}$
$5400 = 500 \cdot v_{B}^{2}$
Step 6: Solve for $v_{B}$
1. Rearranging gives:
$v_{B}^{2} = \frac{5400}{500} = 10.8$
2. Taking the square root:
$v_{B} = \sqrt{10.8} \approx 3.28 m / s$
Final Answer
The velocity of the water coming out of the opening is approximately $3.28 m / s$ .
---

Updated on:7/8/2024

A vessel of area of cross-section A has liquid to a height H . There is a hole at the bottom of vessel having area of cross-section a . The time taken to decrease the level from $H_{1}$ to $H_{2}$ will sec
A $\frac{A}{a} \sqrt{\frac{2}{g}} [\sqrt{H_{1}} - \sqrt{H_{2}}]$
B $\sqrt{2 g h}$
C $\sqrt{2 g h (H_{1} - H_{2})}$
D $\frac{A}{a} \sqrt{\frac{g}{2}} [\sqrt{H_{1}} - \sqrt{H_{2}}$
In the previous question, at the mouth of the tap the area of cross-section is $2.5 c m^{2}$ and the speed of water in $3 m / s$ . The area of cross-section of the water column $80 c m$ below the tap is.
A $2 c m^{2}$
B $1.5 c m^{2}$
C $1 c m^{2}$
D $0.5 c m^{2}$