A ball A of mass 3 kg and a ball B of mass 4 kg are moving alogn the same straight line with speeds of 7m/s and 5 m/s respectively. They approach each other and collide. What is the speed of B after collision, If the coefficient of restitution is 34?
4 m/s
−5 m/s
−4 m/s
6m/s
The correct Answer is:A
To solve the problem, we need to apply the principles of conservation of momentum and the coefficient of restitution. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the given values
- Mass of ball A, mA=3kg
- Mass of ball B, mB=4kg
- Initial speed of ball A, uA=7m/s (approaching)
- Initial speed of ball B, uB=−5m/s (approaching, hence negative)
Step 2: Write the conservation of momentum equation
The total momentum before the collision must equal the total momentum after the collision. Let vA and vB be the final velocities of balls A and B respectively.
mA⋅uA+mB⋅uB=mA⋅vA+mB⋅vB
Substituting the known values:
3⋅7+4⋅(−5)=3⋅vA+4⋅vB
Calculating the left side:
21−20=3vA+4vB
1=3vA+4vB(Equation 1)
Step 3: Write the coefficient of restitution equation
The coefficient of restitution (e) relates the relative speeds of separation and approach. Given e=34:
e=vB−vAuA−uB
Substituting the values:
34=vB−vA7−(−5)
34=vB−vA12
Cross-multiplying gives:
3⋅12=4(vB−vA)
36=4vB−4vA
4vB−4vA=36(Equation 2)
Step 4: Solve the equations
Now we have two equations:
1. 3vA+4vB=1
2. 4vB−4vA=36
From Equation 2, we can express vB:
4vB=36+4vA
vB=9+vA(Equation 3)
Substituting Equation 3 into Equation 1:
3vA+4(9+vA)=1
3vA+36+4vA=1
7vA+36=1
7vA=1−36
7vA=−35
vA=−5m/s
Now substituting vA back into Equation 3 to find vB:
vB=9+(−5)
vB=4m/s
Conclusion
The speed of ball B after the collision is vB=4m/s.
---
- Mass of ball A, mA=3kg
- Mass of ball B, mB=4kg
- Initial speed of ball A, uA=7m/s (approaching)
- Initial speed of ball B, uB=−5m/s (approaching, hence negative)
The total momentum before the collision must equal the total momentum after the collision. Let vA and vB be the final velocities of balls A and B respectively.
1=3vA+4vB(Equation 1)
The coefficient of restitution (e) relates the relative speeds of separation and approach. Given e=34:
34=vB−vA12
36=4vB−4vA
4vB−4vA=36(Equation 2)
Now we have two equations:
2. 4vB−4vA=36
vB=9+vA(Equation 3)
3vA+36+4vA=1
7vA+36=1
7vA=1−36
7vA=−35
vA=−5m/s
vB=4m/s
The speed of ball B after the collision is vB=4m/s.
Topper's Solved these Questions
Similar Questions
Two particle of mass 2kgand1kg are moving along the same straight line with speeds 2m/sand5m/s respectively. What is the speed of the centre of mass of the system if both the particles are moving (a) in same direction (b) in opposite direction ?
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View Solution
Knowledge Check
Two equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
A+4m/s for bothB−3m/sand+5m/sC−4m/sand+4m/sD−5m/sand+3m/sTwo balls A and B having masses 1 kg and 2 kg, moving with speeds 21 m/s and 4 m/s respectively in opposite direction, collide head on. After collision A moves with a speed of 1 m/s in the same direction, then the coefficient of restitution is
A0.1B0.2C0.4DNoneTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
A12 NsB8 NsC20 NsD40 Ns
Two particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
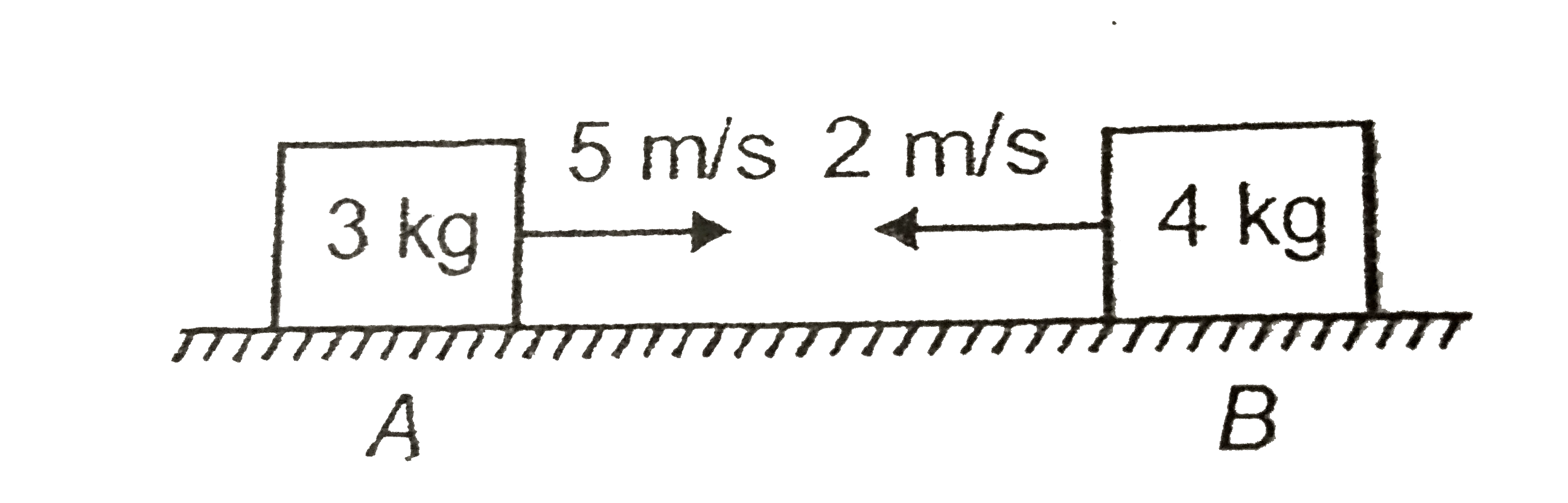
Velocity of A after collision
View SolutionTwo balls of masses 10 kg and 20 kg approach each other with velocities 30 m/s and 20 m/s respectively . Calculate their velocities after they undergo a perfectly eleastic collision .
View SolutionA 10kg ball and a 20kg ball approach each other with velocities 20m/s and 10m/s respectively. What are their velocities after collision, if the collision is perfectly elastic ?
View SolutionTwo particles A and B of masses 10 kg and 38 kg, respectively, are moving along the same straight line with velocities 15 m/s and 3 m/s, respectively, in the same direction. After elastic collision, the velocities of A and B are vAand vB, respectively, in the direction of initial motion. Then

View SolutionTwo spheres of masses 1 kg and 2 kg are moving with velocities of 10 m/s and 5 m/s respectively in the same direction. After the collision the velocity of the lighter sphere decreases by 4 m/s. What is the coefficient of restitution?
View Solution
