A ball is dropped from a height of a height of 90 m on a floor. At each collsion with the floor , the ball loses one - tenth of its speed . Plot the speed -time graph of its motion between t 0 to 12 s.
To solve the problem of plotting the speed-time graph for a ball dropped from a height of 90 m, which loses one-tenth of its speed upon each collision with the floor, we will follow these steps:
Step 1: Calculate the time taken to reach the ground for the first drop.
Using the second equation of motion:
h=ut+12gt2
Since the initial velocity u=0, the equation simplifies to:
h=12gt2
Rearranging gives:
t=√2hg
Substituting h=90m and g=10m/s2:
t=√2×9010=√18≈4.24s
Step 2: Calculate the speed just before the first collision.
Using the first equation of motion:
v=u+gt
Since u=0:
v=gt=10×4.24≈42.4m/s
Step 3: Determine the speed after the first collision.
The ball loses one-tenth of its speed upon collision:
Speed after collision=v×(1−110)=42.4×0.9=38.16m/s
Step 4: Calculate the time taken to reach the ground after the first bounce.
Using the same formula:
t=√2hg
The height after the first bounce can be calculated using the speed just before the bounce:
h=v22g=(38.16)22×10=1454.185620≈72.709m
Now, calculate the time to fall from this new height:
t=√2×72.70910≈√14.5418≈3.81s
Step 5: Repeat the process for subsequent bounces.
1. Second Bounce:
- Speed before collision: 38.16m/s
- Speed after collision: 38.16×0.9≈34.344m/s
- Height after bounce:
h=(34.344)220≈59.5m
- Time to fall:
t=√2×59.510≈3.45s
2. Third Bounce:
- Speed before collision: 34.344m/s
- Speed after collision: 34.344×0.9≈30.9096m/s
- Height after bounce:
h=(30.9096)220≈47.7m
- Time to fall:
t=√2×47.710≈3.09s
Step 6: Continue this process until 12 seconds is reached.
Step 7: Plotting the Speed-Time Graph.
1. Start from t=0 with v=0.
2. At t=4.24s, v=42.4m/s.
3. At t=4.24+3.81≈8.05s, v≈34.344m/s.
4. At t=8.05+3.45≈11.5s, v≈30.9096m/s.
5. The speed will continue to decrease with each bounce until the time reaches 12 seconds.
h=ut+12gt2
Since the initial velocity u=0, the equation simplifies to:
h=12gt2
Rearranging gives:
t=√2hg
t=√2×9010=√18≈4.24s
v=u+gt
Since u=0:
v=gt=10×4.24≈42.4m/s
Speed after collision=v×(1−110)=42.4×0.9=38.16m/s
t=√2hg
The height after the first bounce can be calculated using the speed just before the bounce:
h=v22g=(38.16)22×10=1454.185620≈72.709m
t=√2×72.70910≈√14.5418≈3.81s
- Speed before collision: 38.16m/s
- Speed after collision: 38.16×0.9≈34.344m/s
- Height after bounce:
h=(34.344)220≈59.5m
- Time to fall:
t=√2×59.510≈3.45s
- Speed before collision: 34.344m/s
- Speed after collision: 34.344×0.9≈30.9096m/s
- Height after bounce:
h=(30.9096)220≈47.7m
- Time to fall:
t=√2×47.710≈3.09s
2. At t=4.24s, v=42.4m/s.
3. At t=4.24+3.81≈8.05s, v≈34.344m/s.
4. At t=8.05+3.45≈11.5s, v≈30.9096m/s.
5. The speed will continue to decrease with each bounce until the time reaches 12 seconds.
Similar Questions
A ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take g=10m/s2]
View SolutionA ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View Solution
Knowledge Check
A ball is dropped from a height of 20m on a floor for which e=1/2. The height attained by the ball after the second collision
A1.25mB2.5mC5mD10mA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A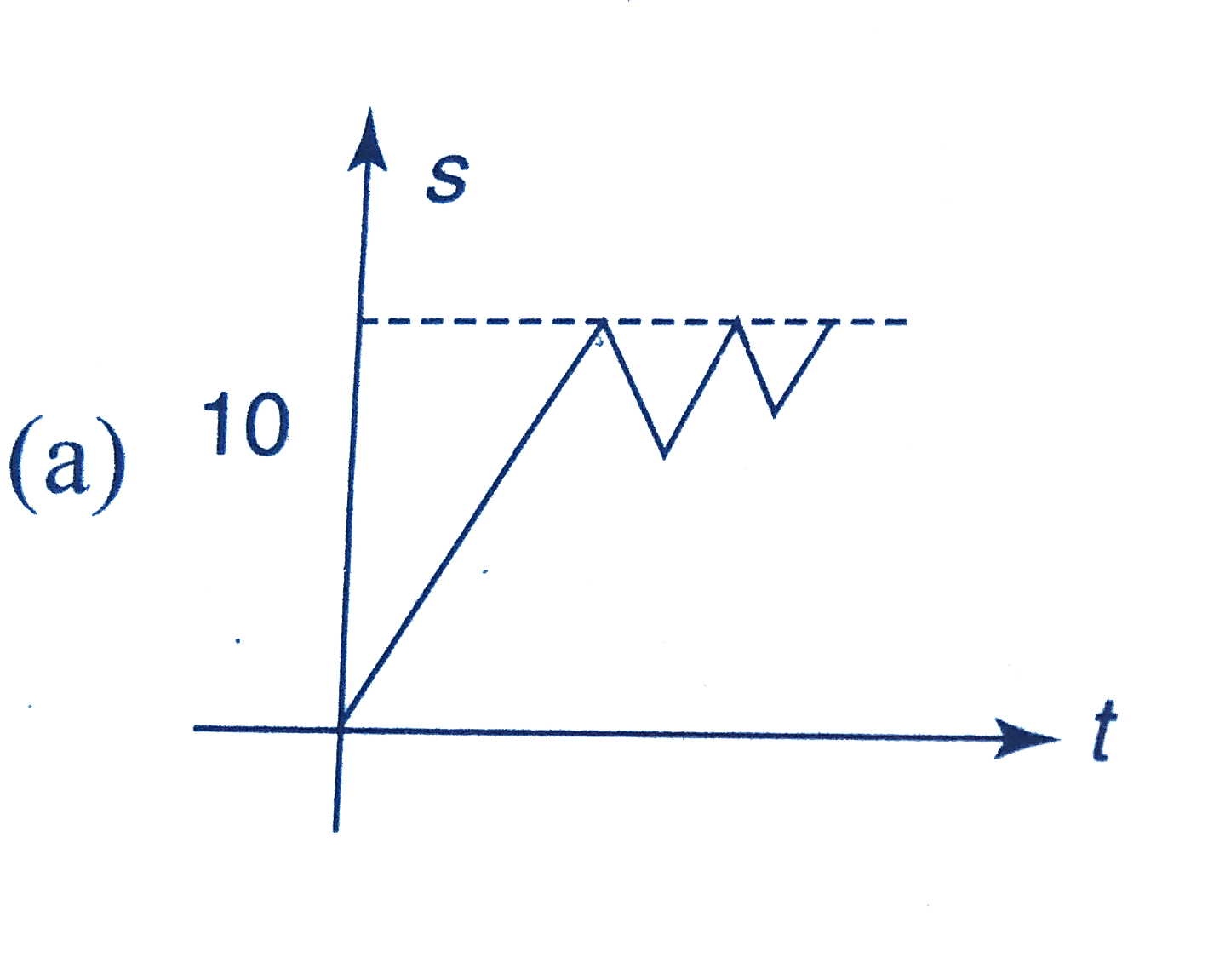 .B
.B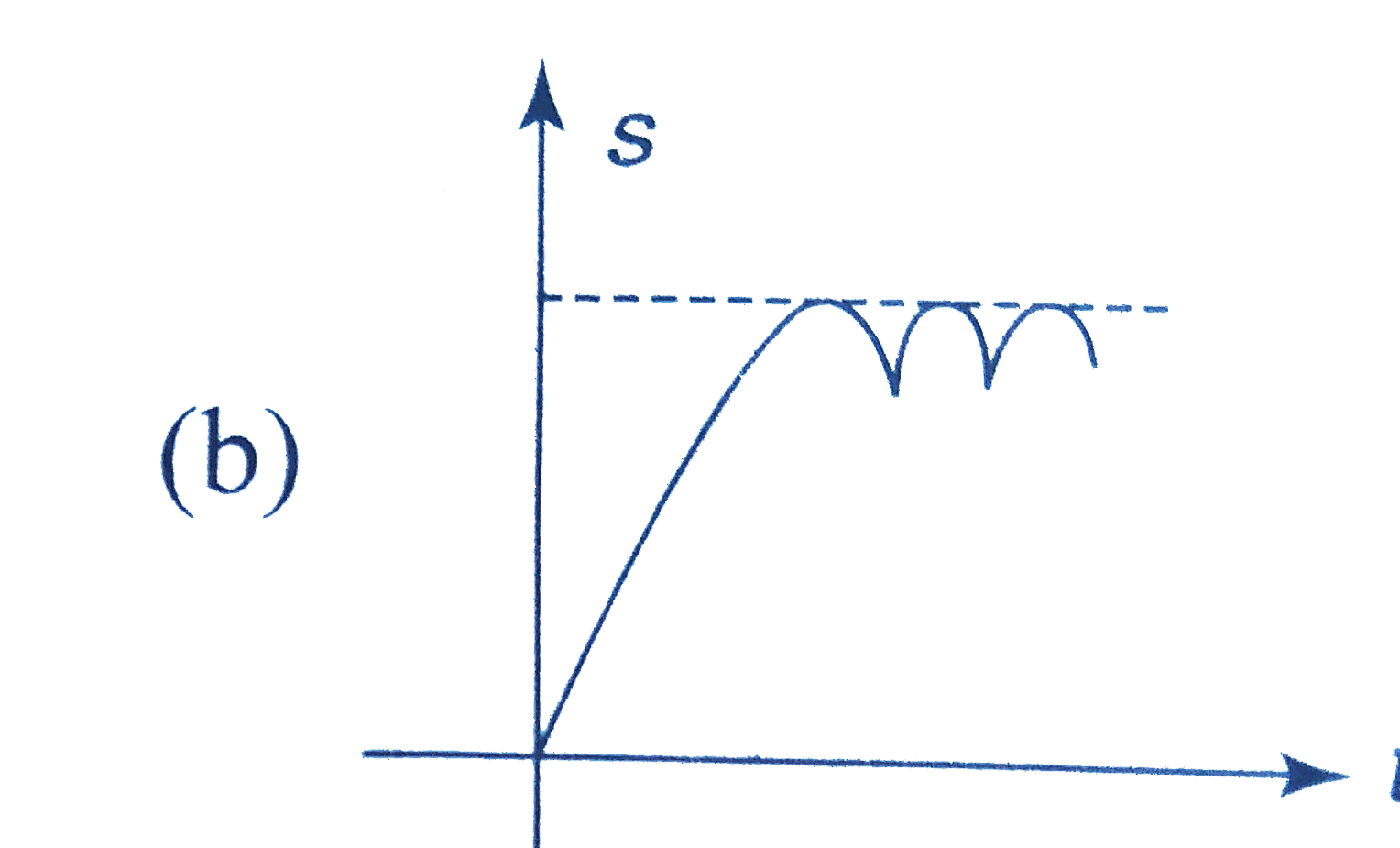 .C
.C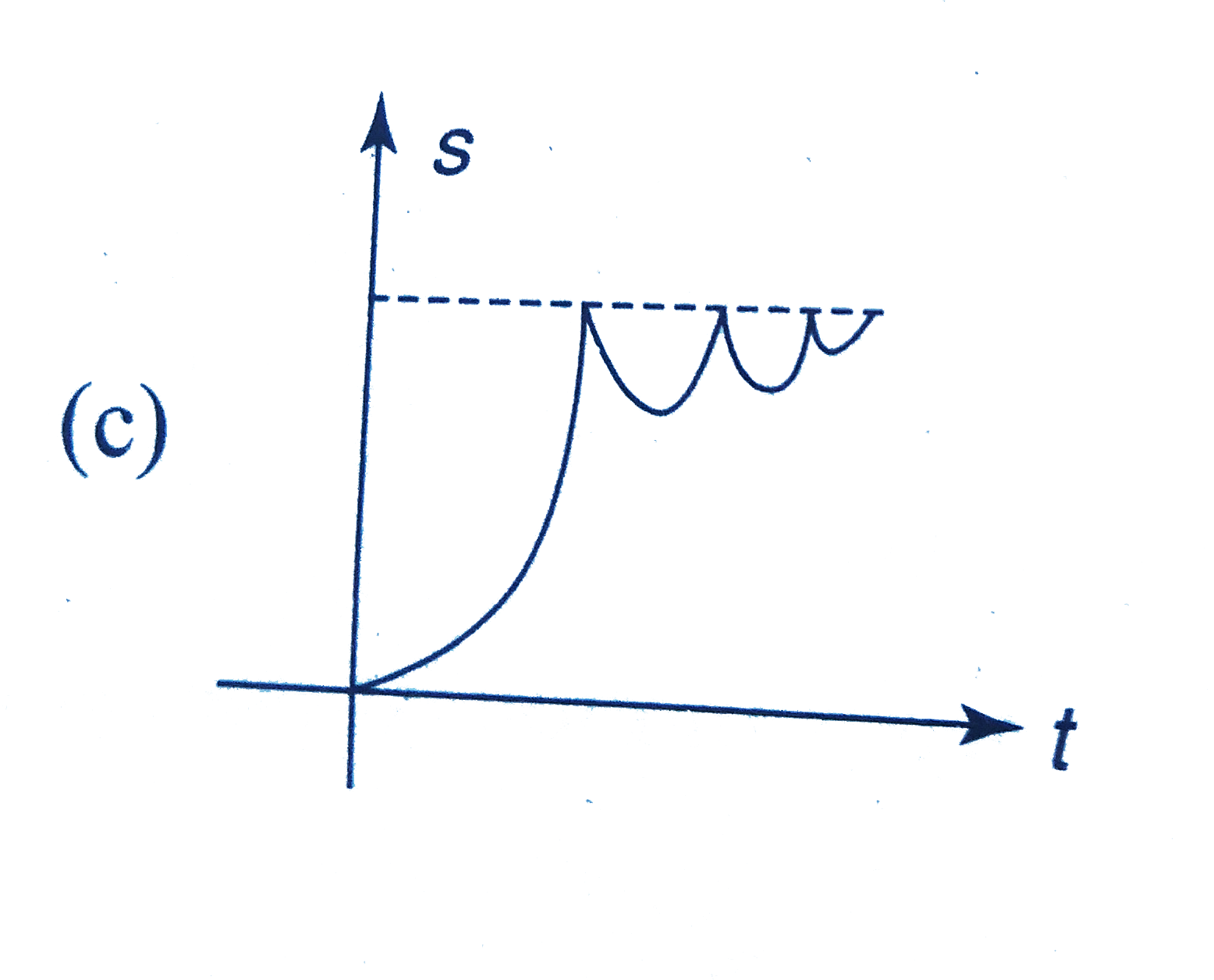 .D
.D .
.A ball is dropped from certain height on a glass floor so that it rebounds elastically to the same height. If the process continues, the velocity -time graph for such a motion would be -
 AIBiiCiiiDiv
AIBiiCiiiDiv
A ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View SolutionA ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
View SolutionIf a ball is dropped from height 2 metre on a smooth eleastic floor, then the time period of oscillation is
View SolutionAn inelastic ball is dropped from a height 100 meter. If due to impact it loses 35% of its energy the ball will rise to a height of
View SolutionA ball is dropped from a height h. As it bounces off the floor, its speed is 80 percent of what it was just before it hit the floor. The ball will then rise to a height of most nearly
View Solution
