A ball is placed on a smooth inclined plane of inclination θ=30∘ to the horizontal, which is rotating at frequency 0.5 Hz about a vertical axiz passing through its lower end. At what distance from the lower end does the ball remain at rest?
0.87m
0.33m
0.5m
0.67m
The correct Answer is:D
ω=2πf=2π(0.5)=πrad s−1
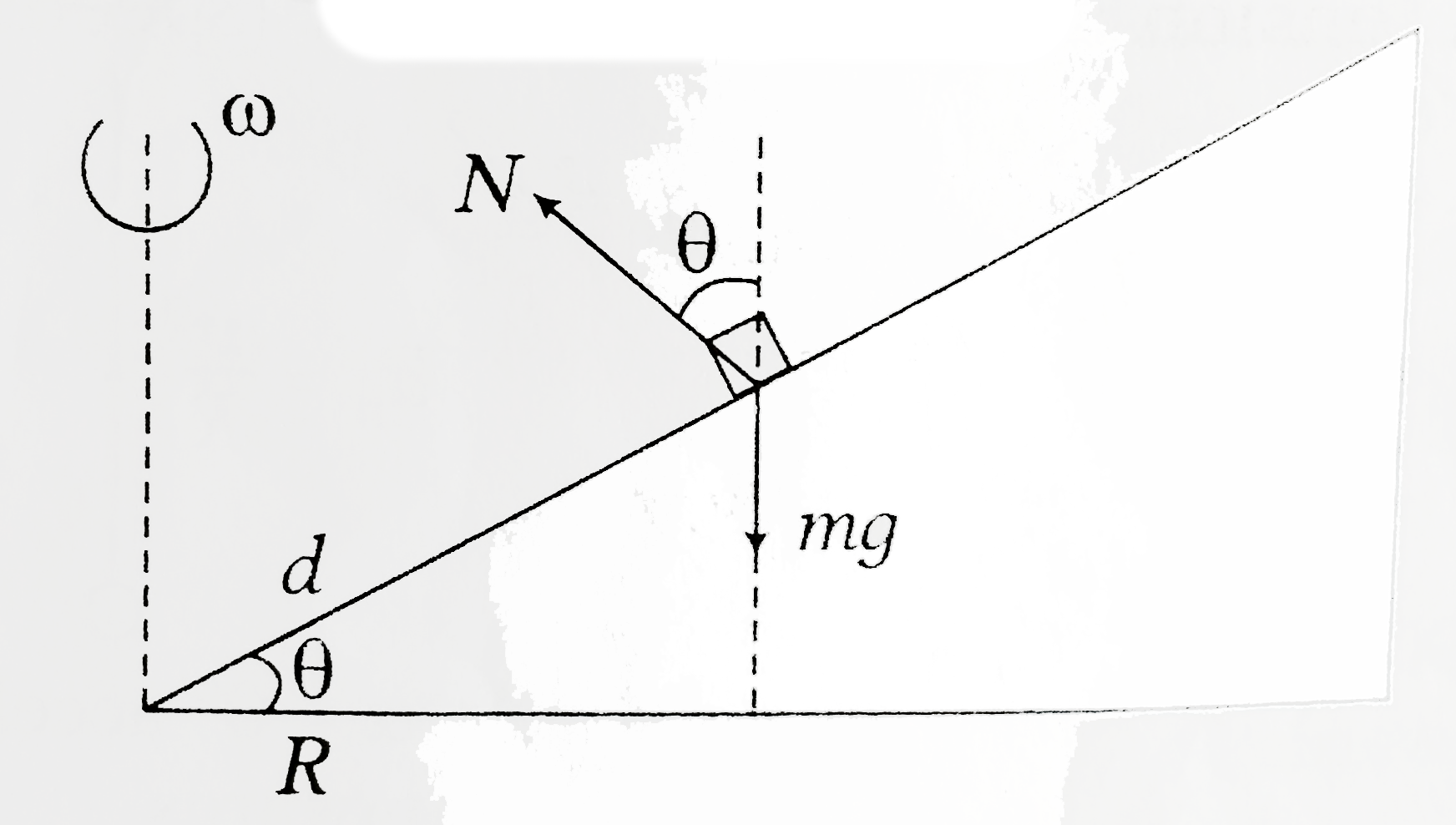
From the figure,
Nsinθ=mRω2 and Ncosθ=mg
or tanθ=Rω2g
∴ R=gtanθω2
⇒ R=10.tan30∘(π2)≈1√3m
Now, d=Rcosθ=1/√3cosθ=1/√3√3/2=23=0.67m
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
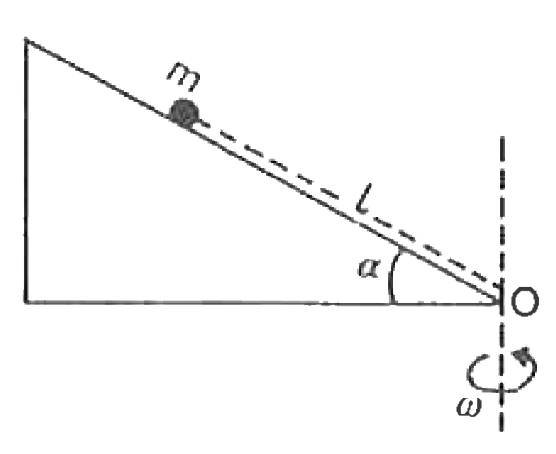
A ball is placed on a smooth chute inclined at an angle α=30∘ to the horizontal and rotating at frequency n=30 rpm about a vertical axis passing through its lower end. At what distance from the end of the chute does the ball rest ?
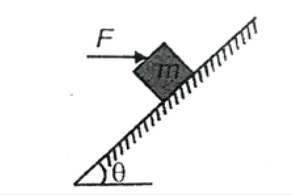
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationA block of mass m is at rest on an incline having an angle of inclination θ with the horizontal. The incline is now being rotated with constant angular velocity ω about an axis passing through the perpendicular side. If the surface of the incline is rough having coefficient of friction as μ, then find the distance 'x' aong the incline so that block just remains stationary with restpect to incline and is on the verge of slipping. [ Take 'x' from the top of the incline as shown in the figure.]
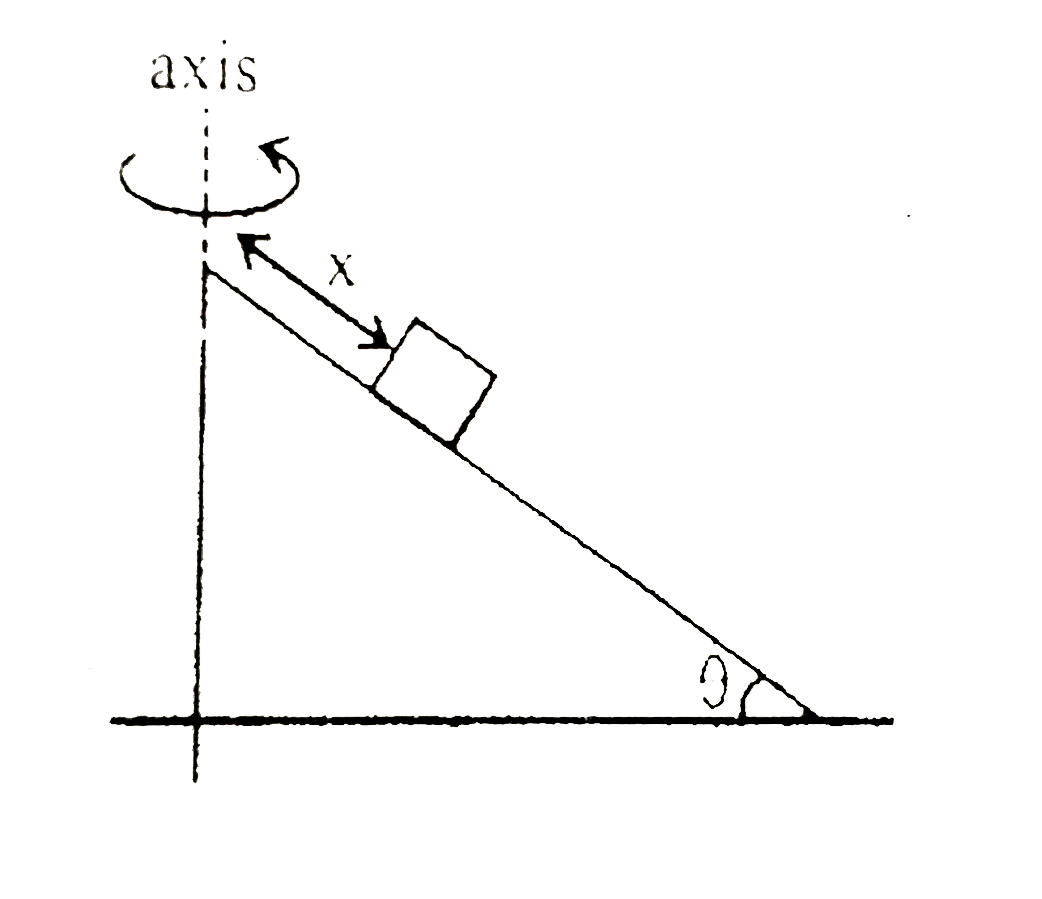 Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1)
Agω2(μ+tanθ)(μtanθ−1)Bgω2(μ−tanθ)(μtanθ+1)Cgω2cosθ(μ−tanθ)(μtanθ+1)Dgω2(μ−tanθ)(μtanθ−1)A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A small block of mass m is tied to the top of a smooth inclined plane with the help of a string of length L as shown in the figure. The inclined plane of inclination θ with horizontal is rotated with an angular velocity ω about a verticle axis passing through the end of the string fixed to the plane.
(a) Find the maximum value of ω so that the block maintains contact with the inclined plane.
(b) Find the ratio of the tension in the string and the normal reaction between the block and the plane.

View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane . At what distance from the impact point will the ball rebound for the second time ?
View SolutionA ball starts falling with zero initial velocity on a smooth inclined plane forming an angle α with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?
View SolutionA smooth inclined plane of length L having inclination θ with the horizontal inside a lift which is moving down with retardation α . The time taken by a body to slide down the inclined plane, from rest, will be
View Solution
