A ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
10√3ms−1
20√3ms−1
10√5ms−1
20√2ms−1
The correct Answer is:C
To solve the problem, we need to analyze the motion of the ball projected at an angle θ with the horizontal. We will use the information given about the angles of motion at specific times to derive the initial velocity of projection.
1. Understanding the Motion:
The ball is projected from the ground at an angle θ. After 1 second, it makes an angle of 45∘ with the horizontal, and after 2 seconds, it moves horizontally.
2. Using the Angle at t=1 second:
At t=1 second, the angle of the velocity vector is 45∘. This means that the vertical and horizontal components of the velocity are equal at this point.
tan(45∘)=1=VyVx
Here, Vy is the vertical component of the velocity at t=1 second, and Vx is the horizontal component.
The vertical component of the velocity can be expressed as:
Vy=Usinθ−g⋅t
Substituting t=1:
Vy=Usinθ−g
The horizontal component remains constant:
Vx=Ucosθ
Setting Vy=Vx gives:
Usinθ−g=Ucosθ
Rearranging this, we get:
Usinθ−Ucosθ=g
U(sinθ−cosθ)=g(Equation 1)
3. Using the Angle at t=2 seconds:
At t=2 seconds, the ball is moving horizontally, which means that the vertical component of the velocity is zero:
Vy=Usinθ−g⋅2=0
Rearranging gives:
Usinθ=2g(Equation 2)
4. Solving the Equations:
Now we have two equations:
- From Equation 1: U(sinθ−cosθ)=g
- From Equation 2: Usinθ=2g
From Equation 2, we can express U:
U=2gsinθ
Substituting U into Equation 1:
2gsinθ(sinθ−cosθ)=g
Dividing both sides by g (assuming g≠0):
2(sinθ−cosθ)sinθ=1
Rearranging gives:
2(sinθ−cosθ)=sinθ
2sinθ−2cosθ=sinθ
sinθ=2cosθ
Dividing both sides by cosθ gives:
tanθ=2
5. Finding the Initial Velocity:
Now substituting tanθ=2 back into Equation 2:
Usinθ=2g
We can express sinθ in terms of tanθ:
sinθ=2√5andcosθ=1√5
Thus,
U=2g2√5=g√5
Final Answer:
The velocity of projection of the ball is:
U=g√5 m/s
The ball is projected from the ground at an angle θ. After 1 second, it makes an angle of 45∘ with the horizontal, and after 2 seconds, it moves horizontally.
At t=1 second, the angle of the velocity vector is 45∘. This means that the vertical and horizontal components of the velocity are equal at this point.
tan(45∘)=1=VyVx
Here, Vy is the vertical component of the velocity at t=1 second, and Vx is the horizontal component.
Vy=Usinθ−g⋅t
Substituting t=1:
Vy=Usinθ−g
Vx=Ucosθ
Usinθ−g=Ucosθ
Rearranging this, we get:
Usinθ−Ucosθ=g
U(sinθ−cosθ)=g(Equation 1)
At t=2 seconds, the ball is moving horizontally, which means that the vertical component of the velocity is zero:
Vy=Usinθ−g⋅2=0
Rearranging gives:
Usinθ=2g(Equation 2)
Now we have two equations:
- From Equation 1: U(sinθ−cosθ)=g
- From Equation 2: Usinθ=2g
U=2gsinθ
2gsinθ(sinθ−cosθ)=g
Dividing both sides by g (assuming g≠0):
2(sinθ−cosθ)sinθ=1
Rearranging gives:
2(sinθ−cosθ)=sinθ
2sinθ−2cosθ=sinθ
sinθ=2cosθ
Dividing both sides by cosθ gives:
tanθ=2
Now substituting tanθ=2 back into Equation 2:
Usinθ=2g
We can express sinθ in terms of tanθ:
sinθ=2√5andcosθ=1√5
Thus,
U=2g2√5=g√5
The velocity of projection of the ball is:
U=g√5 m/s
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A ball is projected with velocity (u) at an anle α with horizontal plane. What is its speed when it makes an angle θ whith the horizontal plane ?
View SolutionA ball is thrown at an angle θ with the horizontal. Its time of flight is 2 s. Its horizontal range is 100 m. What is the horizontal component of velocity of projection ? Take g=10ms−2.
View Solution
Knowledge Check
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its accelerationBits velocity becomes zero at its maximum height.Cits velocity makse zero angle with the horizontal at its maximum heightDthe body just before hitting the ground, the direction of velocity coincides with the accelerationA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
Av0√3gB√3v0gCv0gDv0gA shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
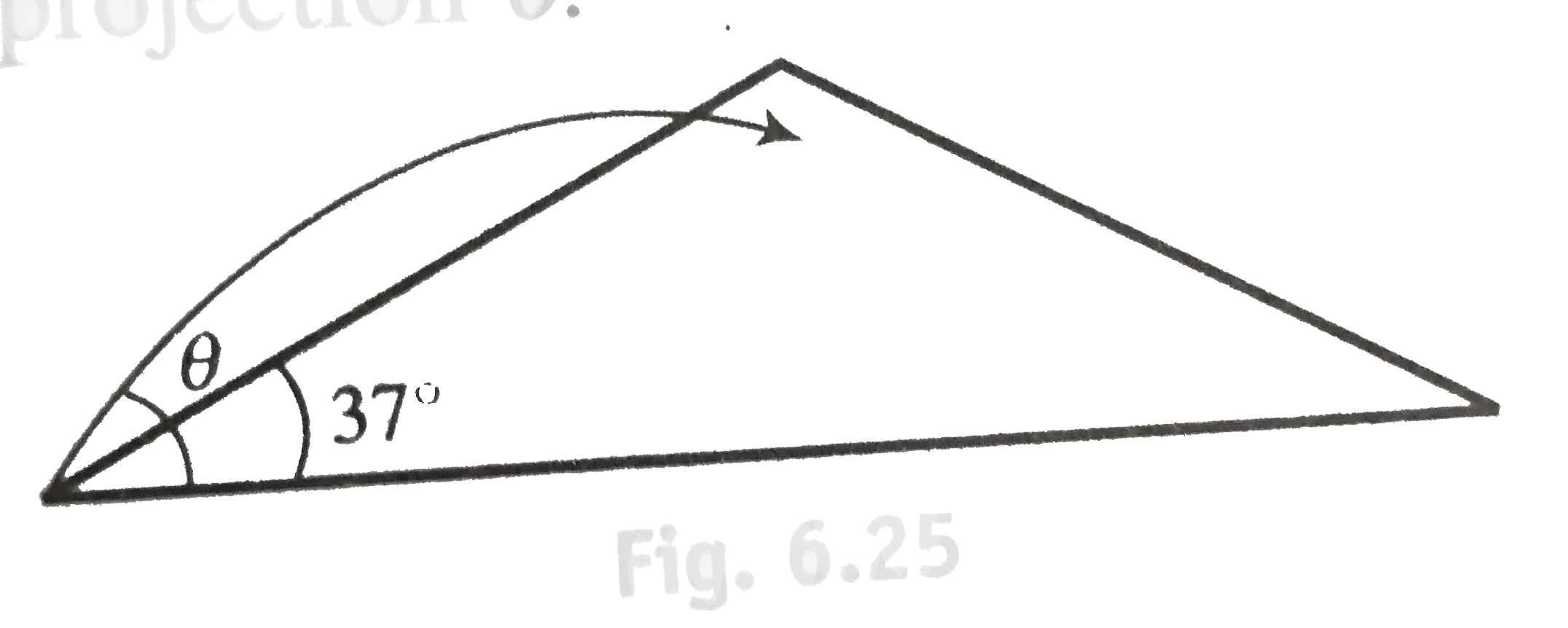 Atanθ=25Btanθ=38Ctanθ=32DNone of these
Atanθ=25Btanθ=38Ctanθ=32DNone of these
A particle is projected from the ground . One second after the projection, the particle is found to be moving at an angle 45∘ with the horizontal . Speed of the particle becomes minimum two seconds after the projection . If angle of projection is tan−1(n), then what is the value of n ?
View SolutionA projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA ball is projected at an angle 60∘ with the horizontal with speed 30 m/s. What will be the speed of the ball when it makes an angle 45∘ with the horizontal ?
View Solution
