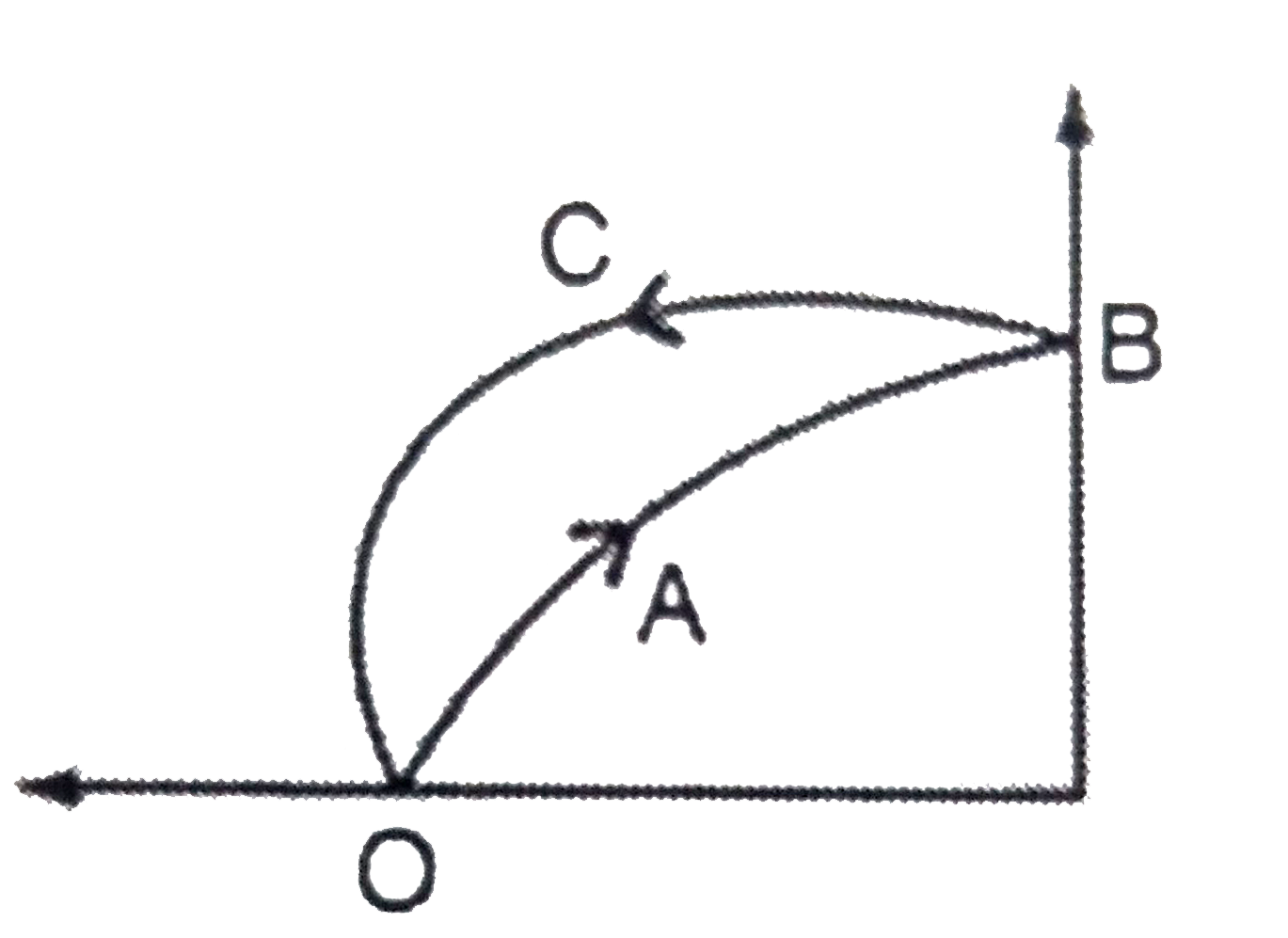
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
The correct Answer is:A, B
As we have discussed in the theory, the horizontal component of the velocity of ball duing the path OAB is ucosα while in its return jouney BCO it is eucosα. The time of flight T also remains unchanged. Hence,
T=tOAB+tBCO
or 2usinαg=aucosα+aeucosα
aeucosα=2u2sinαcosα−aggucosα
e=ag2u2sinαcosα−ag
or e=1(u2sin2αag−1)

Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A ball projected from the ground with speed 10m/s at an angle of 45∘ with horizontal. It collides with a wall at a distance 2 m from the point of projection and returns to its original position. If the coefficient of restitution between the ball and wall is 1/x, find x.
View SolutionA ball is given velocity u=√3gd at an angle 45∘ with horizontal. It strikes a wall at distance d and returns to its original position. Find the coefficient of restitution e.
View Solution
Knowledge Check
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is
 Aaeucosα,u2sin2α2gBaucosα,u2sin2α2gCaeucosα,u2sin2α2gDaucosα,u2sin2α2g
Aaeucosα,u2sin2α2gBaucosα,u2sin2α2gCaeucosα,u2sin2α2gDaucosα,u2sin2α2gAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
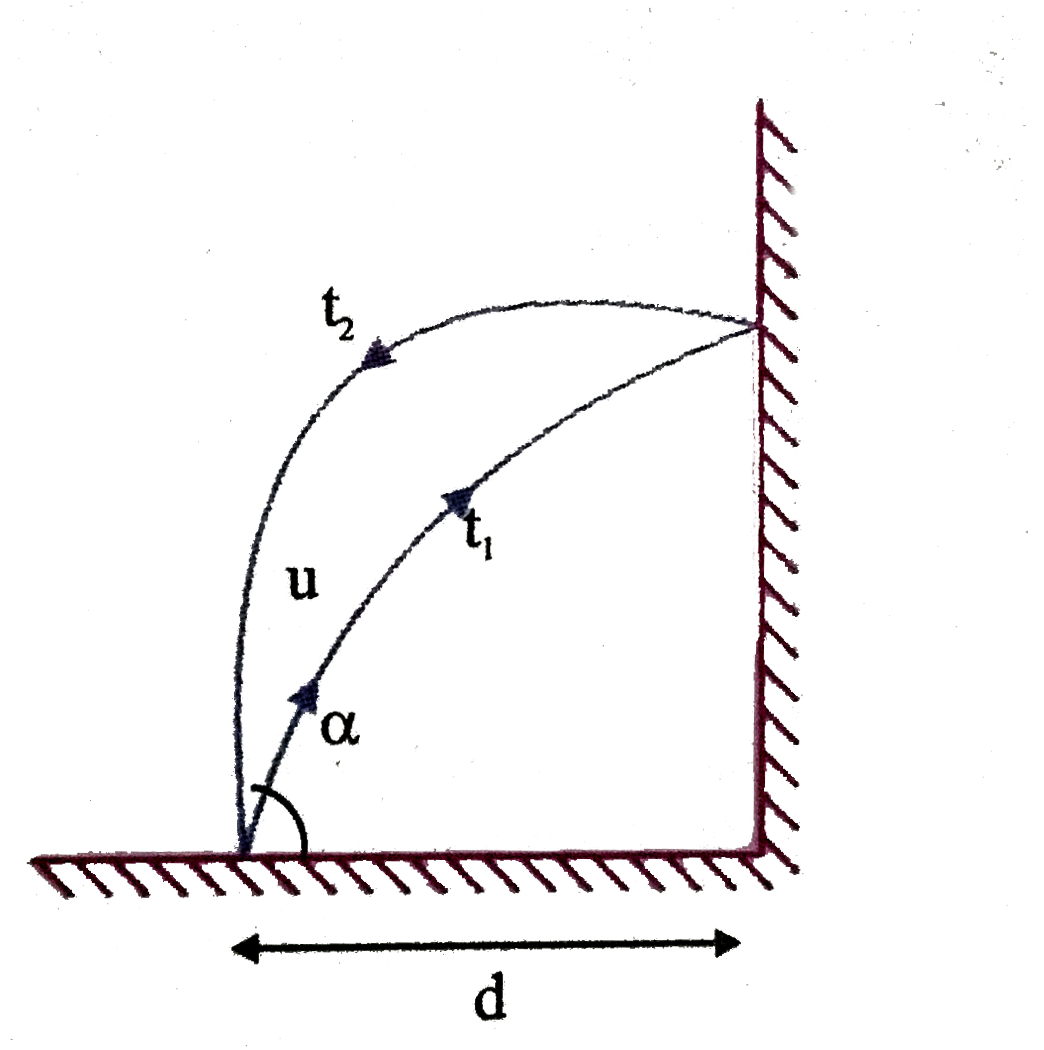
The horizontal distance 'd' from the wall isAu2sin2αg(e1+e)Bu2sinαg(e1+e)Cu2cos2αg(e1+e)Du2sin2α2g(e1+e)An inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
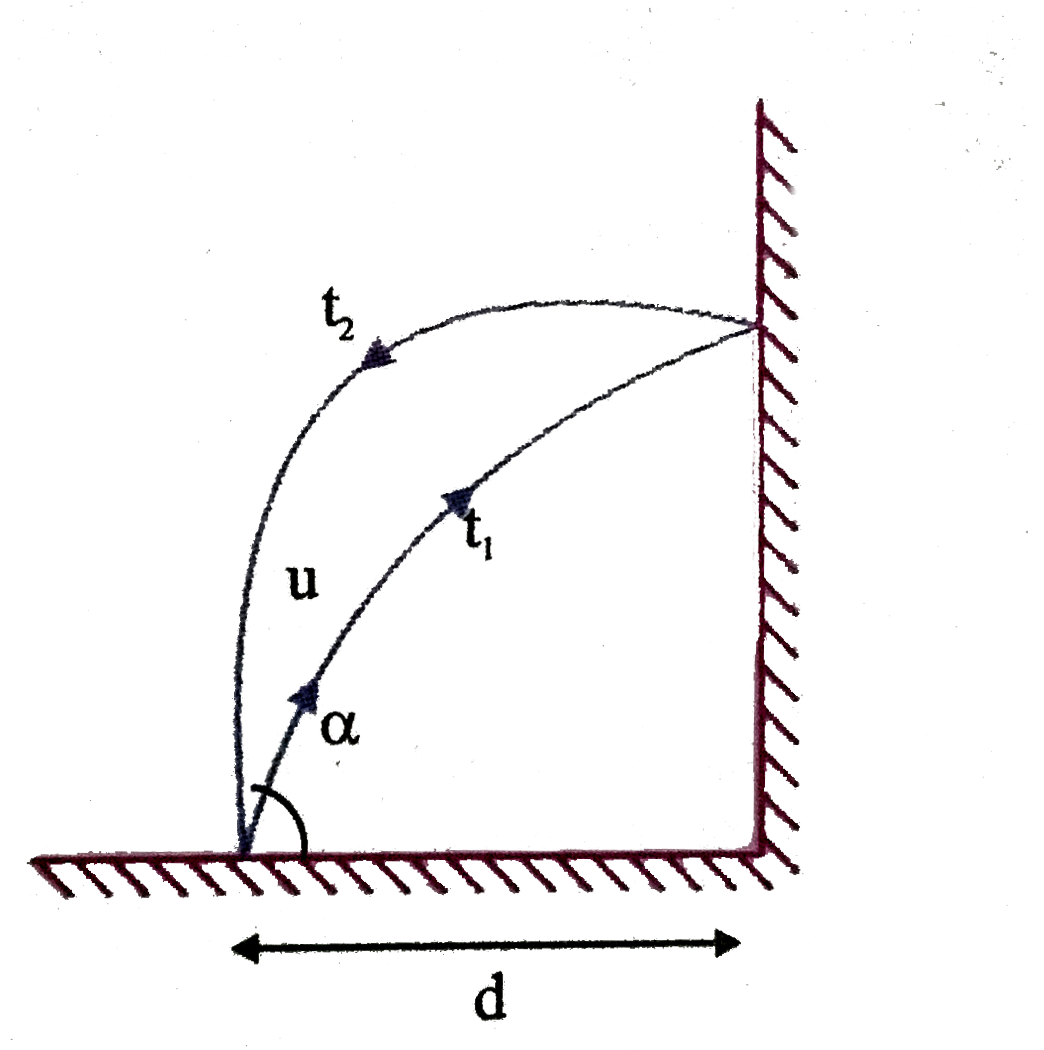
If the line joining the point of projection and the point of impact makes an angle 'θ' with the horizontal, then tanθ isAetanαB(1+e)tanαC(1+e)tanαDtanα(1+e)
A small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA ball is projected from ground with a speed of 20ms−1 at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height of
View SolutionAn inelastic ball is projetced with a velocity 'u' at an angle 'α' to the horizontal, towards a wall distant 'd' from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is 'e')
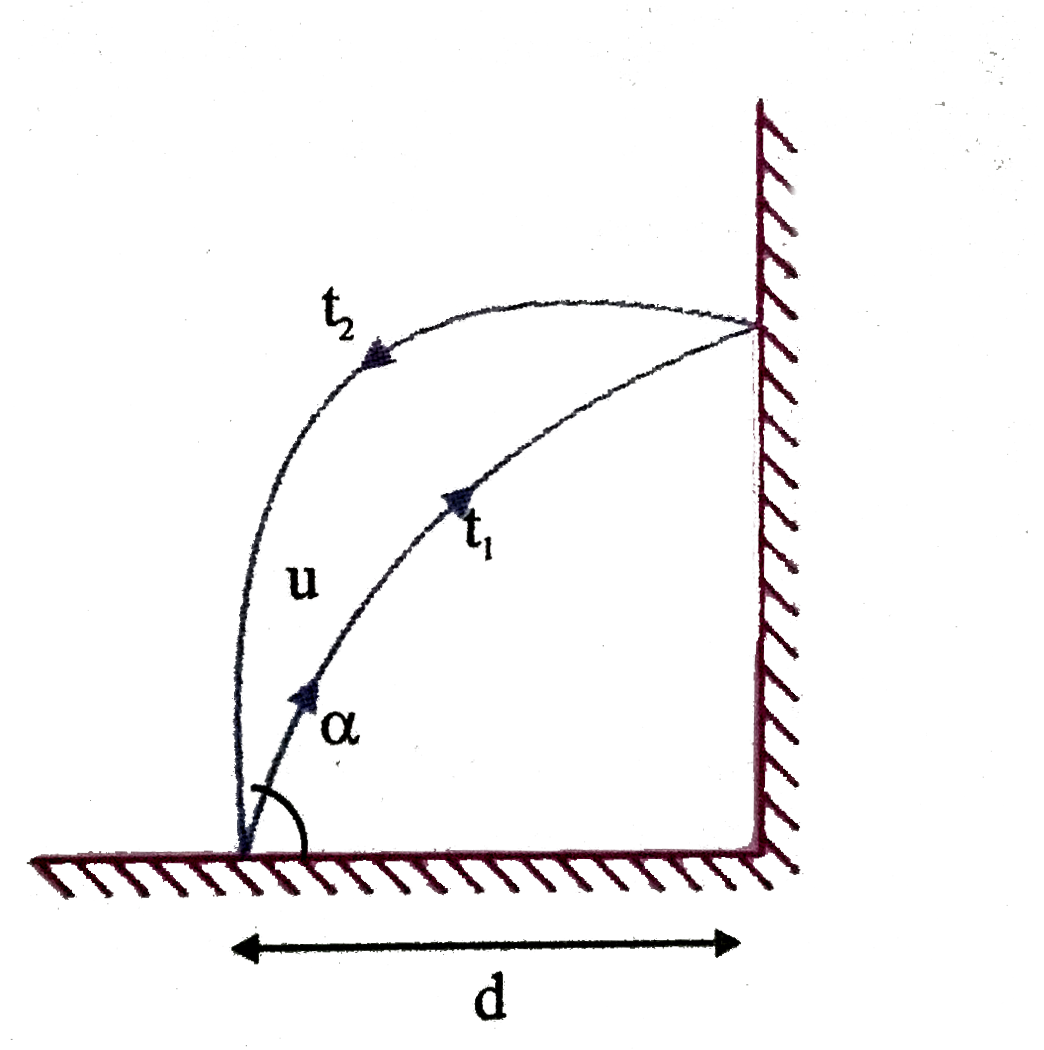
The total time of journey of the ball is
View SolutionA ball is projected from the ground with velocity u such that its range is maximum Then
View Solution
