A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the total time of journey of ball.
To solve the problem of finding the total time of journey of a ball thrown vertically upwards to a height of 20 m and then returning to the ground, we can follow these steps:
Step 1: Understand the motion of the ball
The ball is thrown upwards, reaches a maximum height, and then falls back to the ground. The total time of the journey consists of the time taken to ascend (t1) and the time taken to descend (t2).
Step 2: Use the equations of motion
We can use the second equation of motion:
s=ut+12at2
where:
- s is the distance (height in this case),
- u is the initial velocity,
- a is the acceleration (which will be -g during ascent and +g during descent),
- t is the time.
Step 3: Analyze the ascent
At the maximum height, the final velocity is 0. Therefore, we can find the time of ascent (t1) using the following relation:
h=ut1+12(−g)t21
Since we do not know u yet, we will first find t2 (the time of descent).
Step 4: Analyze the descent
For the descent, we can use the same equation:
h=0⋅t2+12gt22
Here, h=20 m, g=10m/s2, and the initial velocity u=0 at the maximum height.
Substituting the values:
20=0⋅t2+12⋅10⋅t22
This simplifies to:
20=5t22
Step 5: Solve for t2
Rearranging gives:
t22=205=4
Taking the square root:
t2=√4=2s
Step 6: Find t1
Since the time of ascent (t1) is equal to the time of descent (t2):
t1=t2=2s
Step 7: Calculate the total time of journey
The total time t is the sum of the time of ascent and the time of descent:
t=t1+t2=2+2=4s
Final Answer
The total time of the journey of the ball is 4 seconds.
---
The ball is thrown upwards, reaches a maximum height, and then falls back to the ground. The total time of the journey consists of the time taken to ascend (t1) and the time taken to descend (t2).
We can use the second equation of motion:
s=ut+12at2
where:
- s is the distance (height in this case),
- u is the initial velocity,
- a is the acceleration (which will be -g during ascent and +g during descent),
- t is the time.
At the maximum height, the final velocity is 0. Therefore, we can find the time of ascent (t1) using the following relation:
h=ut1+12(−g)t21
Since we do not know u yet, we will first find t2 (the time of descent).
For the descent, we can use the same equation:
h=0⋅t2+12gt22
Here, h=20 m, g=10m/s2, and the initial velocity u=0 at the maximum height.
20=0⋅t2+12⋅10⋅t22
This simplifies to:
20=5t22
Rearranging gives:
t22=205=4
Taking the square root:
t2=√4=2s
Since the time of ascent (t1) is equal to the time of descent (t2):
t1=t2=2s
The total time t is the sum of the time of ascent and the time of descent:
t=t1+t2=2+2=4s
The total time of the journey of the ball is 4 seconds.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXAMPLES
24 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(A)
19 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - TOPIC 3 (3 Marks Questions )
7 Videos
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- LIGHTBOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )
9 Videos
Similar Questions
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the initial velocity of the ball
View SolutionA ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the final velocity of ball on reaching the ground
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the initial velocity of the ball .
Take g = 9.8 ms−2
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the final velocity of the ball when it strikes the ground.
Take g = 9.8 ms−2
View SolutionA ball is thrown vertically upwards. It returns 6 s later. Calculate the greatest height reached by the ball
View SolutionA ball is thrown vertically upwards. It was observed at a height h twice after a time interval Δt. The initial velocity of the ball is
View SolutionA ball of mass m is thrown straight up. It goes to a maximum height and then returns. Finally it strikes ground. In the whole process.
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
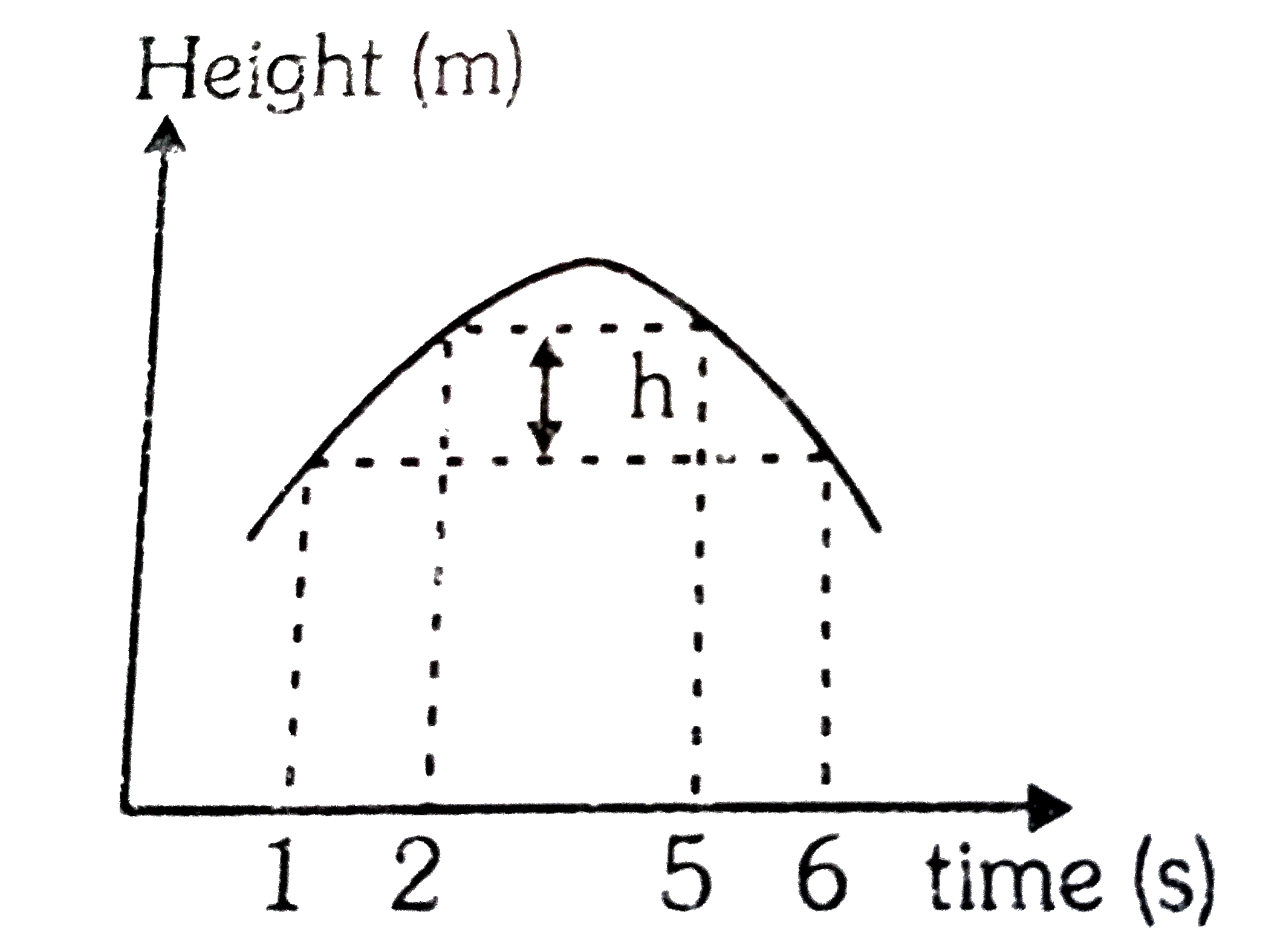
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA ball is thrown vertically upwards with a velocity of 10 ms−1. It returns to the ground with a velocity of 9 ms−1. If g=9.8 ms−2 , then the maximum height attained by the ball is nearly (assume air resistance to be uniform)
View Solution
