A ball of mass $1 k g$ moving with a velocity of $5 m / s$ collides elastically with rough ground at an angle $θ$ with the vertical as shown in Fig. What can be the minimum coefficient of friction if ball rebounds vertically after collision? (given $tan θ = 2$ )

Text Solution

Verified by Experts

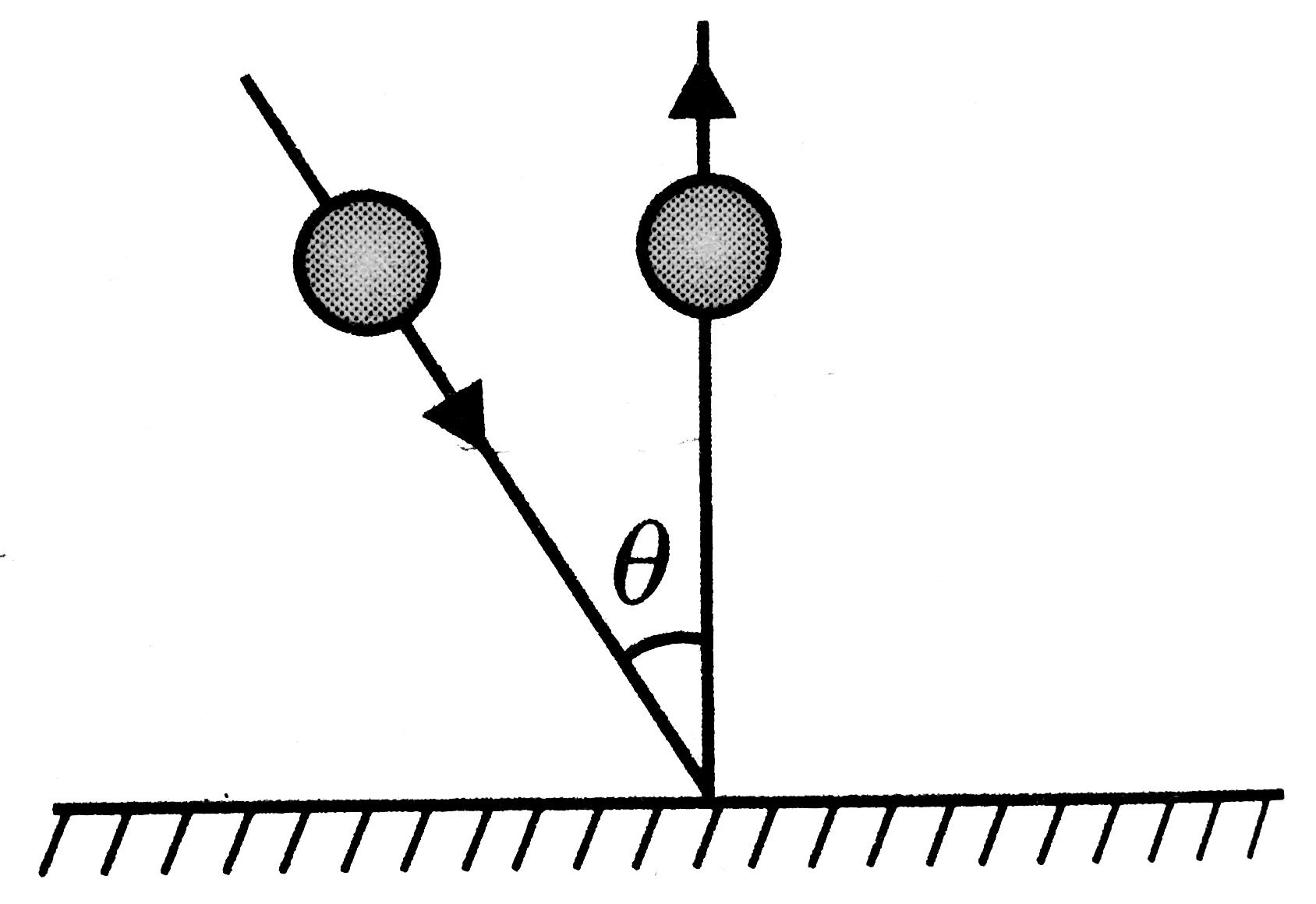
The correct Answer is:1

From impulse momentum theorem
$\int N d t = m (v + 5 cos θ)$ ………….i
$\int f d t = m 5 sin θ$
$μ \int N d t = m 5 sin θ$ ……..ii
$\Rightarrow μ m (v + 5 cos θ) = m 5 sin θ$

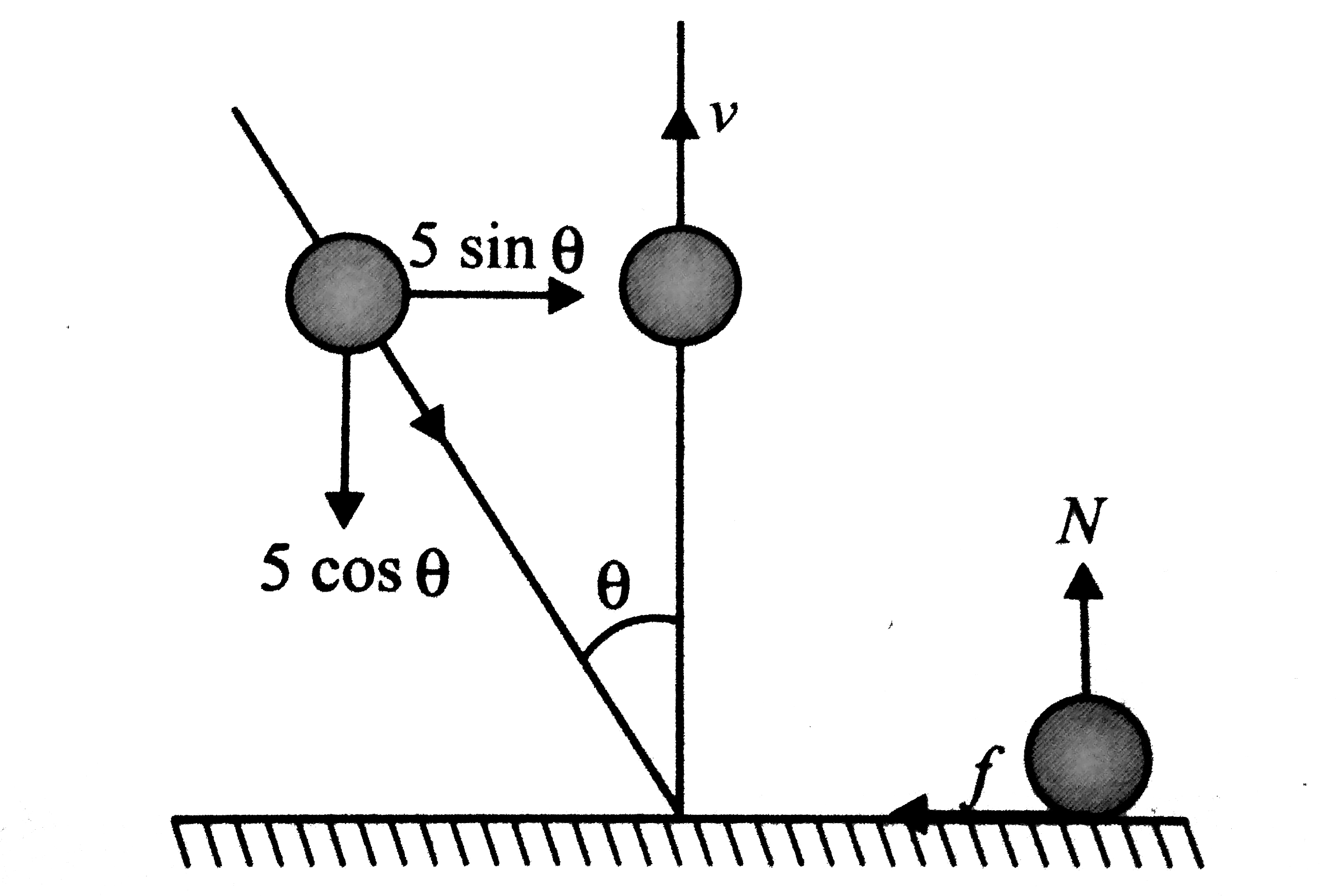
According to Newton's law of restitution
$v = 35 cos θ$
Solve to get $μ = 1$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ball of mass $M$ moving with a velocity $v$ collides perfectly inelastically with another ball of same mass but moving with a velocity $v$ in the opposite direction. After collision
Aboth the balls come to rest
Bthe velocities are exchanged between the two balls
Cboth of them move at right angles to the original line of motion
Done ball comes to rest and another ball travels back with velocity $2 v$
Question 2 - Select One
A ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
A $- v, 2 v$
B $- 2 v, v$
C $v, - 2 v$
D $2 v, - v$
Question 3 - Select One
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is $v_{1}$ and velocity of second ball after collision is $v_{2}$ then
A $v_{1} = \frac{(1 - e) u}{2}, v_{2} = \frac{(1 + e) u}{2}$
B $v_{1} = \frac{(1 + e) u}{2}, v_{2} = \frac{(1 - e) u}{2}$
C $v_{1} = \frac{u}{2}, v_{2} = - \frac{u}{2}$
D $v_{1} = (1 + e) u, v_{2} = (1 - e) u$

CENGAGE PHYSICS-CENTRE OF MASS-Integer

Home
Ask Doubt
Profile