A ball of mass M is hanging from the lower end of a string of length l. a bullet of mass m moving horizontally hits the ball and sticks to it. What should be the minimum velocity of the bullet so that the ball will be able to complete a full circle ?
The correct Answer is:M+mm√5gl
Topper's Solved these Questions
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - PROBLEM SET -II (Hots Numerical Problems)
9 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - ENTRANCE CORNER (Assertion-reason type)
7 Videos
- WORK AND ENERGYBOOK - CHHAYA PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - PROBLEM SET -I
49 Videos
- WBCHSE QUESTION PAPER -2019BOOK - CHHAYA PUBLICATIONCHAPTER - WBCHSE QUESTION PAPER -2019EXERCISE - SECTION - II ( GROUP -D)
10 Videos
Similar Questions
A ball of mass 10−2kg and having charge +3×10−6C is tied at one end of a 1m along thread. The other end of the thread is fixed and a charge −3×10−6C is placed at this end. The ball can move in the circulr orbit of radius 1m in the vertical plane. Initially, the ball is at the bottom. Find the minimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View SolutionA ball of mass 10−2kg and having charge +3×10−6C is tied at one end of a 1m along thread. The other end of the thread is fixed and a charge −3×10−6C is placed at this end. The ball can move in the circulr orbit of radius 1m in the vertical plane. Initially, the ball is at the bottom. Find the monimum initial horizontal velocity of the ball, so that it will be able to complete the full circle.
View Solution
Knowledge Check
A bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
A100m/sB150m/sC200m/sD250m/sA uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
A2[√2gl]B√2glC2[√gl]D√glA ball of mass M is rotating in a conical pendulum by a string of length L. If radius of circular path is L√2, find the velocity of mass
A√gLB√gL2C√2gLD√gL√2
A uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionAn insect jumps from ball A onto ball B, which are suspended from inextensible light strings each of length L=8cm. The mass of each ball and insect is same. What should be the minimum relative velocity (in ms−1) of jump of insect w.r.t. ball A, if both the balls manage to complete the full circle?
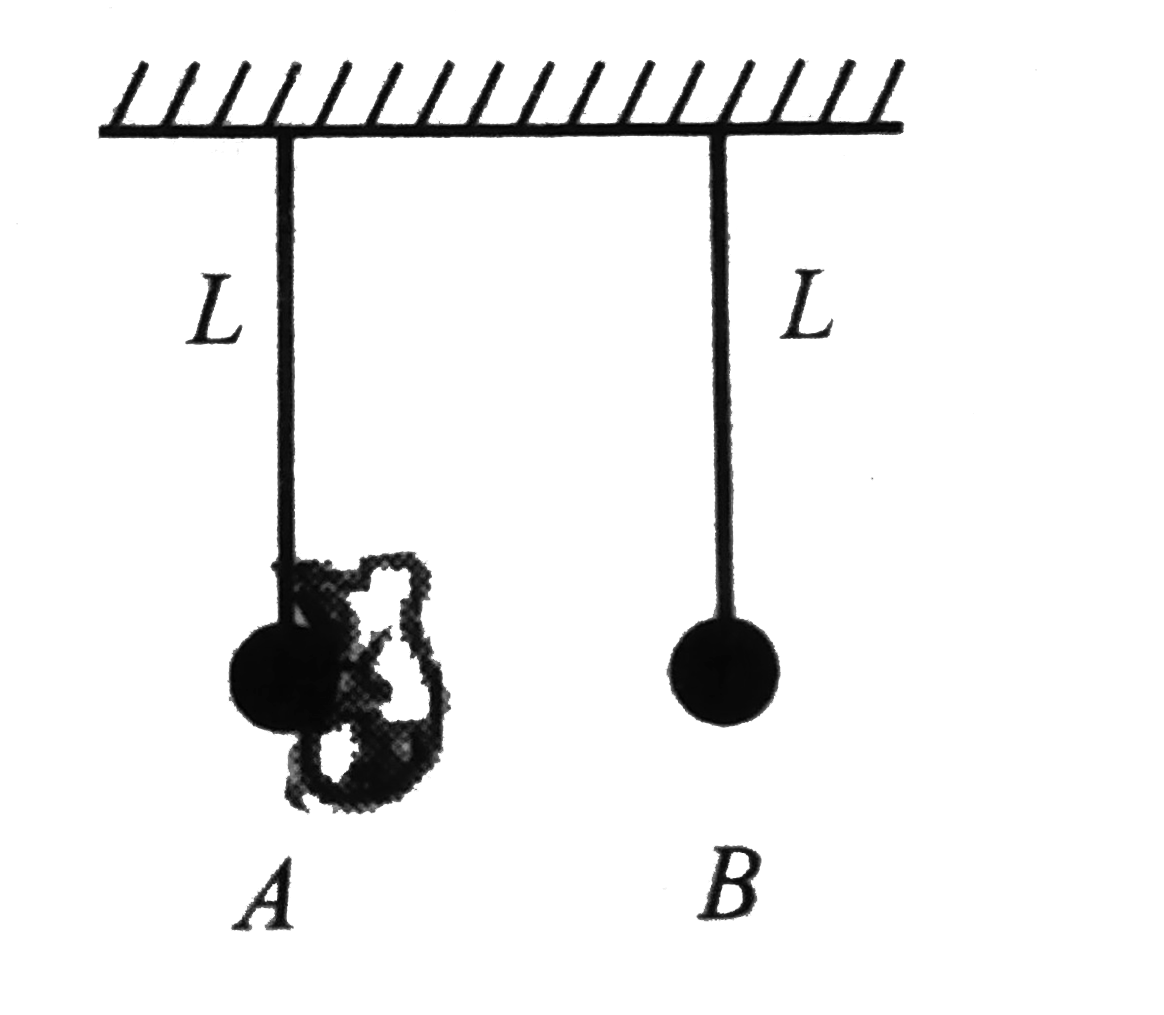
View SolutionAn insect jumps from ball A onto ball B, which are suspended from inextensible light strings each of length L=8cm. The mass of each ball and insect is same. What should be the minimum relative velocity (in ms−1) of jump of insect w.r.t. ball A, if both the balls manage to complete the full circle?

View SolutionA mass m is tied to a string of length l and is rotated in a vertical circle with centre at the other end of the string.
(a) Find the minimum velocity of the mass at the top of the circle so that it is able to complete the circle.
(b) Find the minimum velocity at the bottom of the circle corresponding to the above condition.
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View Solution
