A ball of mass $m_{1}$ moving with a certain speed collides elastically with another ball of mass $m_{2}$ kept at rest . If the first ball starts moving in reversed direction after the impact then

A

$m_{1} = m_{2}$

B

$m_{1} > m_{2}$

C

$m_{1} < m_{2}$

D

None of these

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem, we need to analyze the elastic collision between two balls, where one ball (mass $m_{1}$ ) is moving and the other ball (mass $m_{2}$ ) is at rest. After the collision, the first ball moves in the reverse direction. We will derive the conditions under which this scenario occurs.
1. Define Initial Conditions:
- Let the mass of the first ball be $m_{1}$ and its initial velocity be $u_{1} = u$ .
- Let the mass of the second ball be $m_{2}$ and its initial velocity be $u_{2} = 0$ (since it is at rest).
2. Apply Conservation of Momentum:
- According to the law of conservation of momentum, the total momentum before the collision must equal the total momentum after the collision.
- Initial momentum: $m_{1} u + m_{2} \cdot 0 = m_{1} u$
- Final momentum: $m_{1} v_{1} + m_{2} v_{2}$
- Therefore, we have the equation:
$m_{1} u = m_{1} v_{1} + m_{2} v_{2} (1)$
3. Apply Conservation of Kinetic Energy:
- Since the collision is elastic, kinetic energy is also conserved.
- Initial kinetic energy: $\frac{1}{2} m_{1} u^{2} + 0 = \frac{1}{2} m_{1} u^{2}$
- Final kinetic energy: $\frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2}$
- Therefore, we have the equation:
$\frac{1}{2} m_{1} u^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} (2)$
4. Use the Coefficient of Restitution:
- The coefficient of restitution $e$ for elastic collisions is 1. It is defined as:
$e = \frac{Relative velocity of separation}{Relative velocity of approach} = 1$
- This gives us:
$v_{2} - v_{1} = u_{1} - u_{2} \Rightarrow v_{2} - v_{1} = u (3)$
5. Substitute Equation (3) into Equation (1):
- From equation (3), we can express $v_{2}$ in terms of $v_{1}$ :
$v_{2} = v_{1} + u$
- Substitute this into equation (1):
$m_{1} u = m_{1} v_{1} + m_{2} (v_{1} + u)$
- Simplifying this gives:
$m_{1} u = m_{1} v_{1} + m_{2} v_{1} + m_{2} u$
$m_{1} u - m_{2} u = (m_{1} + m_{2}) v_{1}$
$(m_{1} - m_{2}) u = (m_{1} + m_{2}) v_{1} (4)$
6. Determine the Condition for Reversed Direction:
- For the first ball to move in the reverse direction, $v_{1}$ must be negative:
$v_{1} < 0$
- From equation (4), if $u > 0$ (initial velocity of $m_{1}$ is positive), then for $v_{1}$ to be negative, we need:
$m_{1} - m_{2} < 0 \Rightarrow m_{1} < m_{2}$
Conclusion:
The condition that must be fulfilled for the first ball to start moving in the reverse direction after the elastic collision is:
$m_{1} < m_{2}$

|

Updated on:18/9/2024

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object of mass $M_{1}$ moving horizontally with speed u collides elastically with another object of mass $M_{2}$ at rest. Select correct statement.

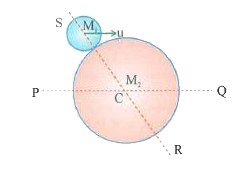AThe momentum of system is conserved only in direction PQ
BMomentum of $M_{1}$ is conserved in direction perpendicular to SR
CMomentum of $M_{2}$ will change in direction normal to CR
DAll of these
Question 2 - Select One
A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
AMv
Bmv
C $\frac{M m}{M + m} v$
D $\frac{M^{2}}{M + m} v$
Question 3 - Select One or More
A ball of mass $m_{1}$ , collides elastically and head on with ball of mass $m_{2}$ at rest. Then
AThe transfer of kinetic energy to the second ball is maximum when $m_{1} = m_{2}$
BThe change of momentum of first ball is maximum, when $m_{1} < < m_{2}$ .
CThe velocity of the second ball is maximum, when $m_{1} > > m_{2}$ .
DNone of these

MODERN PUBLICATION-WORK, ENERGY AND POWER -Objective Type Questions (A. Multiple Choice Questions)

Home
Ask Doubt
Profile