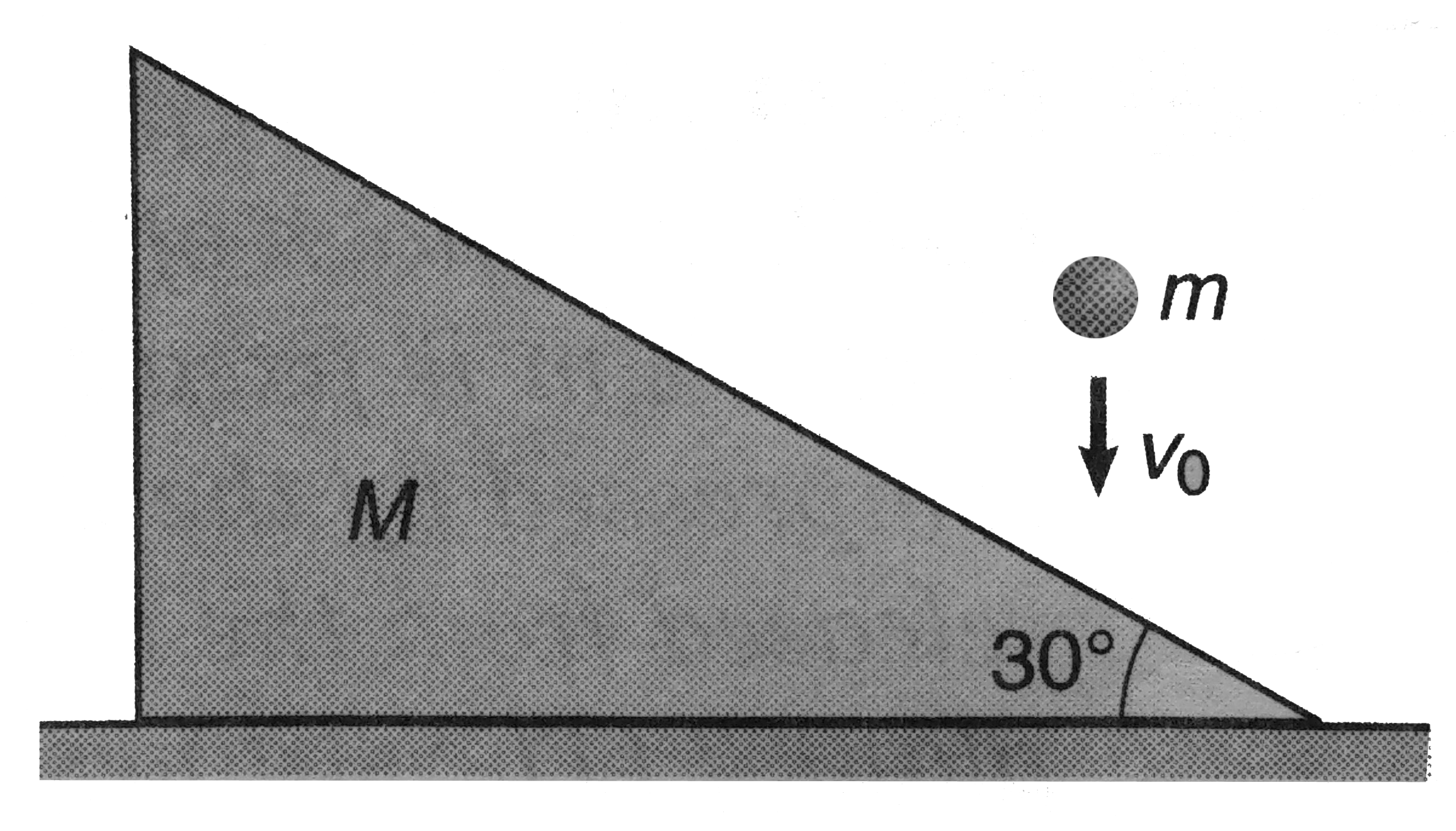
A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept on a smooth, horizontal surface as shown in figure. If impulse between ball and wedge during collision is J. Then make two equations which relate J with velocity components of wedge and ball. Also find impulse on wedges from ground during impact.
The correct Answer is:A
Given M=2kg and m=1kg
Let, J be the impulse between ball and wedge during collision and v1, v2 and v3 be the components of velocity of the wedge and the ball in horizontal and vertical directions respectively.

Applying impulse=change in momentum
we get Jsin30∘=Mv1=mv2
or J2=2v1=v2...(i)
Jcos30∘=m(v3+v0)
or √32J=(v3+2) ...(ii)
So these are two equations relating J and velocity components of wedge and ball. Further, net vertical impulse on wedge should be zero. Therefore, impulse on wedge from ground is Jsin30∘ or J2 in upward direction.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
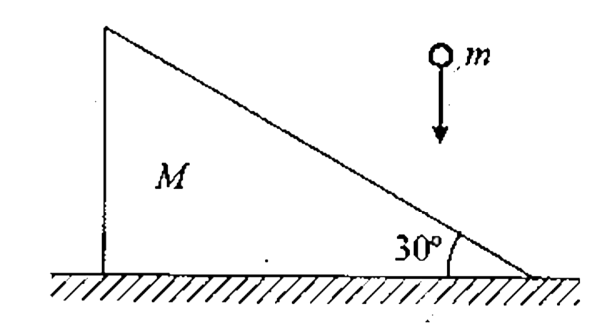
A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
View SolutionA particle of mass m strikes normally to a stationary wedge of mass 5m kept on the smooth horizontal surface as shown.If the particle sticks to the wedge then loss in kinetic energy of the system during collision is?
View Solution
Knowledge Check
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2NsA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the aboveA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. It h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
 AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
AMhcotθM+mB(b) mhcotθM+mC(c) MhcosecθM+mD(d) mhcosecθM+m
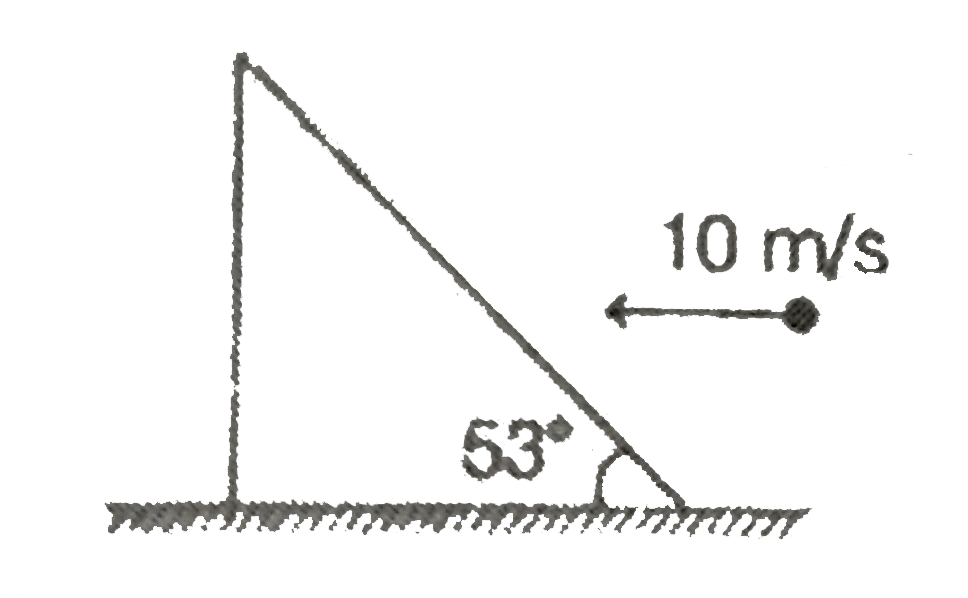
A ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA small particle of mass m=2kg moving with constant horizontal velocity u=10m/s strikes a wedge shaped block of mass M=4kg placed on smooth horizontal surface on its inclined surface as shown in figure. After collision particle starts moving up the inclined plane. Calculate the velocity of wedge immediately after collision.
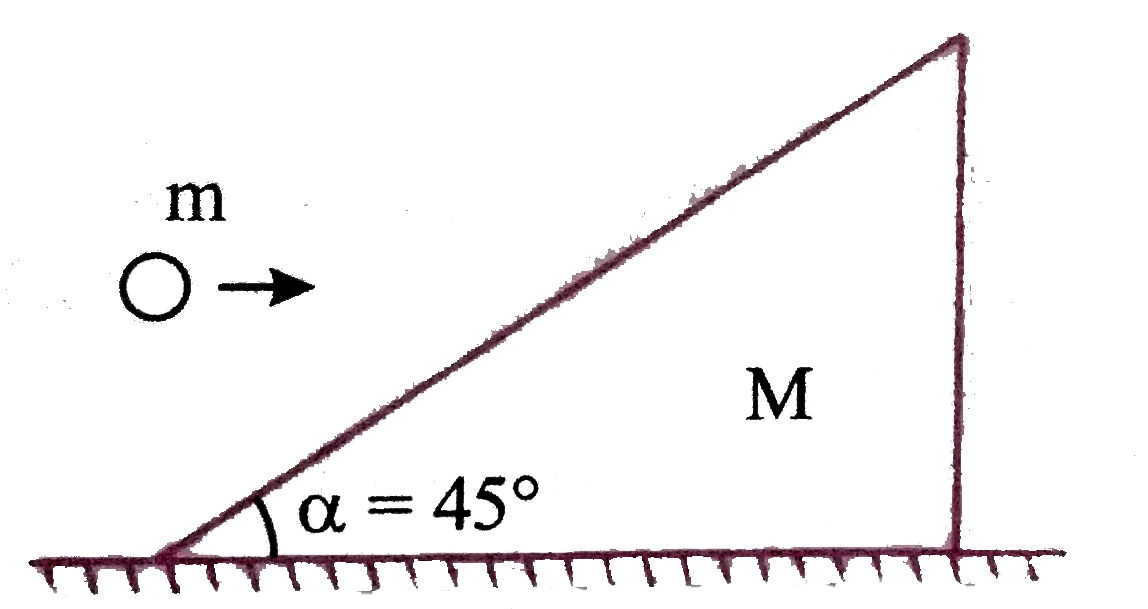
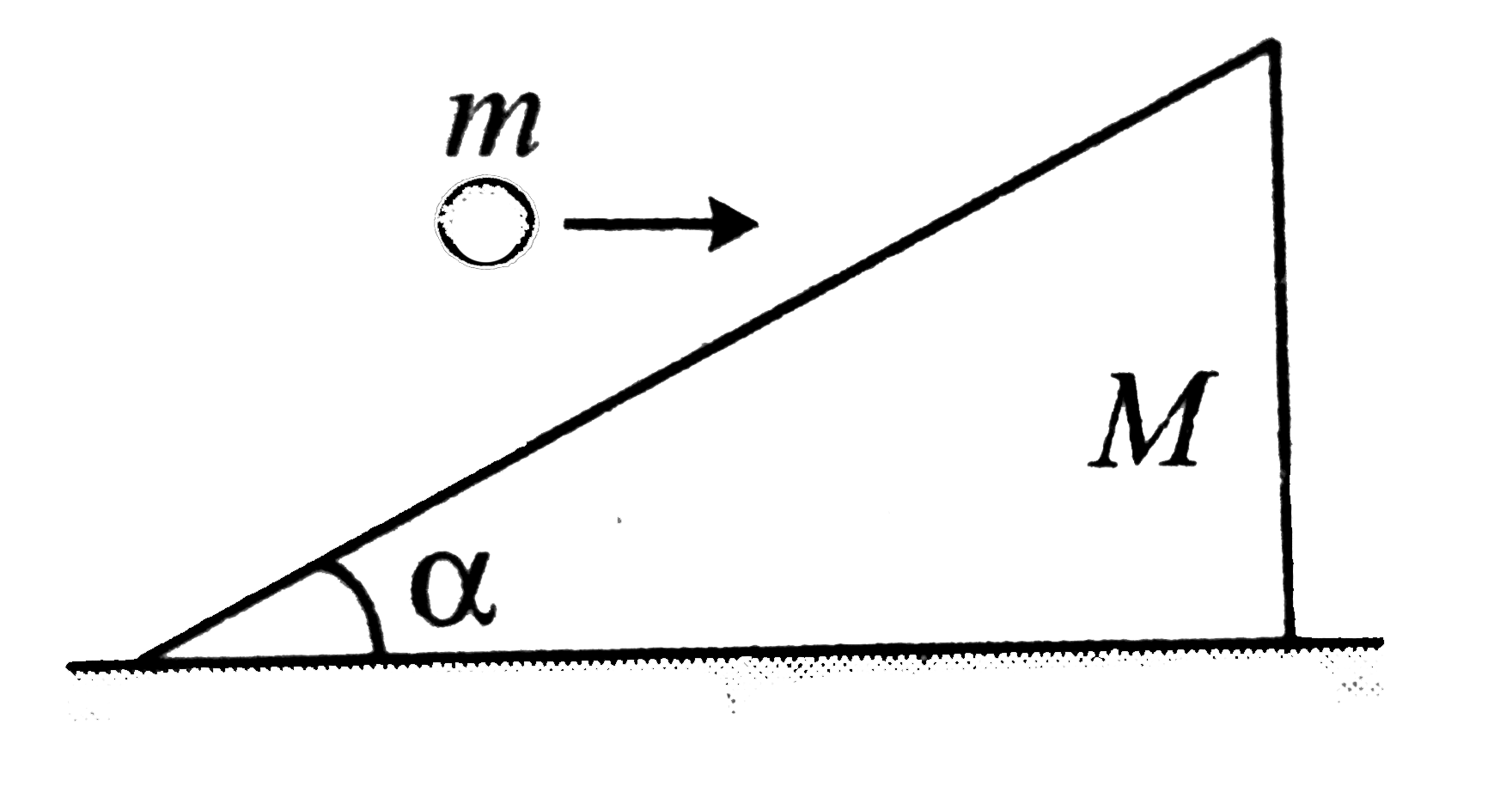
View SolutionA ball of mass m moving with constant horizontal velocity u strikes a stationary wedge of mass M on its inclined surface as shown in the figure. After collision, the ball starts moving up the inclined plane. The wedge is placed on frictionless horizontal surface.
a. Calculate the velocity of wedge immediately after collision.
b. Calculate the maximum height the ball can ascend on the wedge.
View SolutionA ball of mass m moving horizotally which velocity u hits a wedge of mass M. The wedge is situated on a smooth horizontal source. If after striking with wedge the ball starts moving in vertical direction and the wedge starts moving in horizotal plane. calculate
a. the velocity of wedge V.
b. the velocity (v) at which the ball moves in vertical direction.
c. the impulse imparted by the ball on the wedge.
d. the coefficient of restitution e=?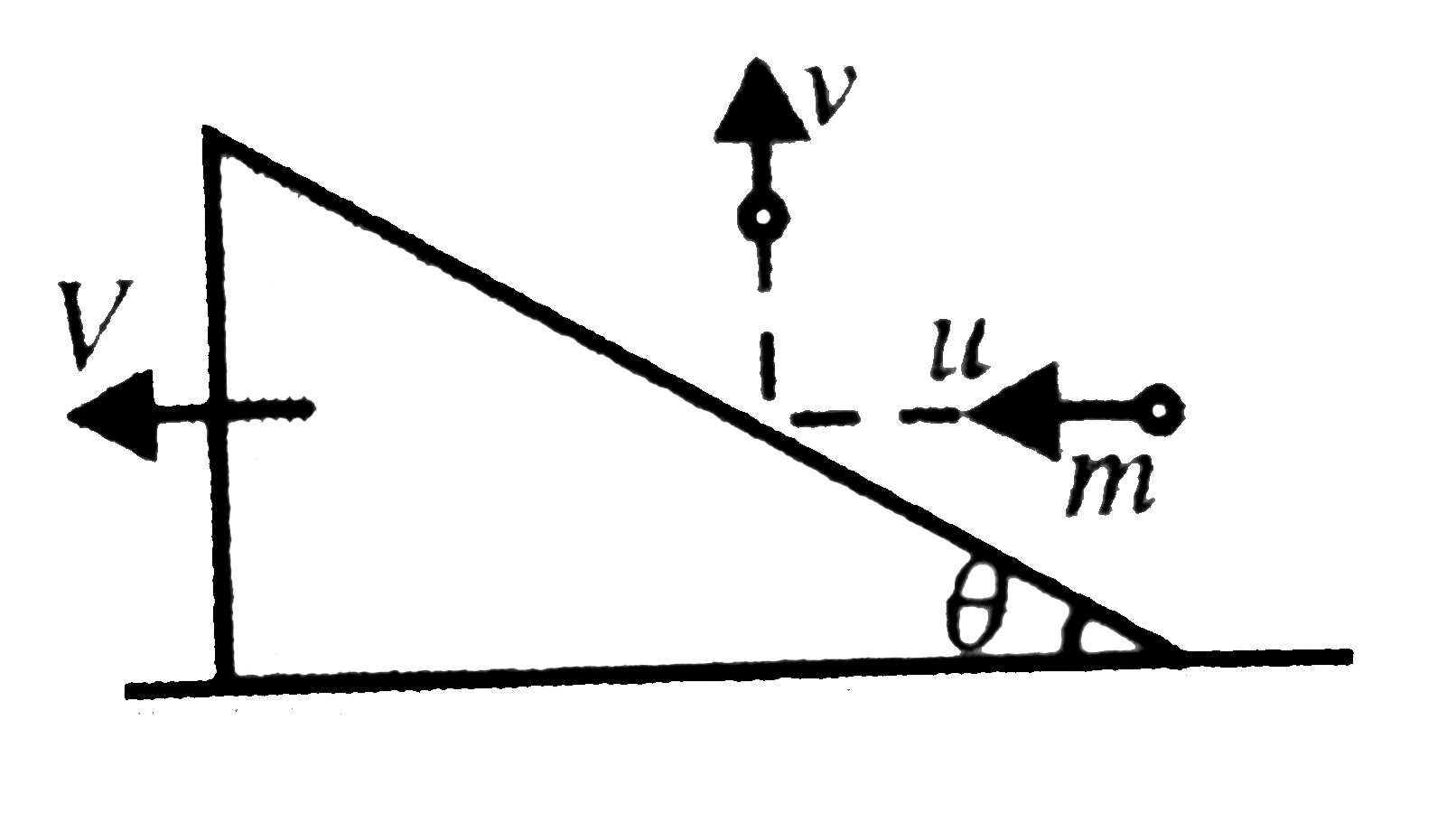
View SolutionA 250 g ball moving horizontally with velocity 10.0m/s strikes inclined surface of a 720g smooth wedge as shown in the figure. The wedge is placed at rest on a frictionless horizontal ground. If the coefficient of restitution is 0.8, calculate the velocity of the wedge after the impact.

View Solution
