A ball (solid sphere) is thrown down the valley in such a way that it slides with a speed $v_{0}$ initially without rolling. Prove that it will roll without any sliding when its speed falls to $(\frac{5}{7}) v_{0}$ . The transition from pure sliding to pure rolling is gradual, so that both sliding and rolling take place during this interval.

Video Solution

Text Solution

Verified by Experts

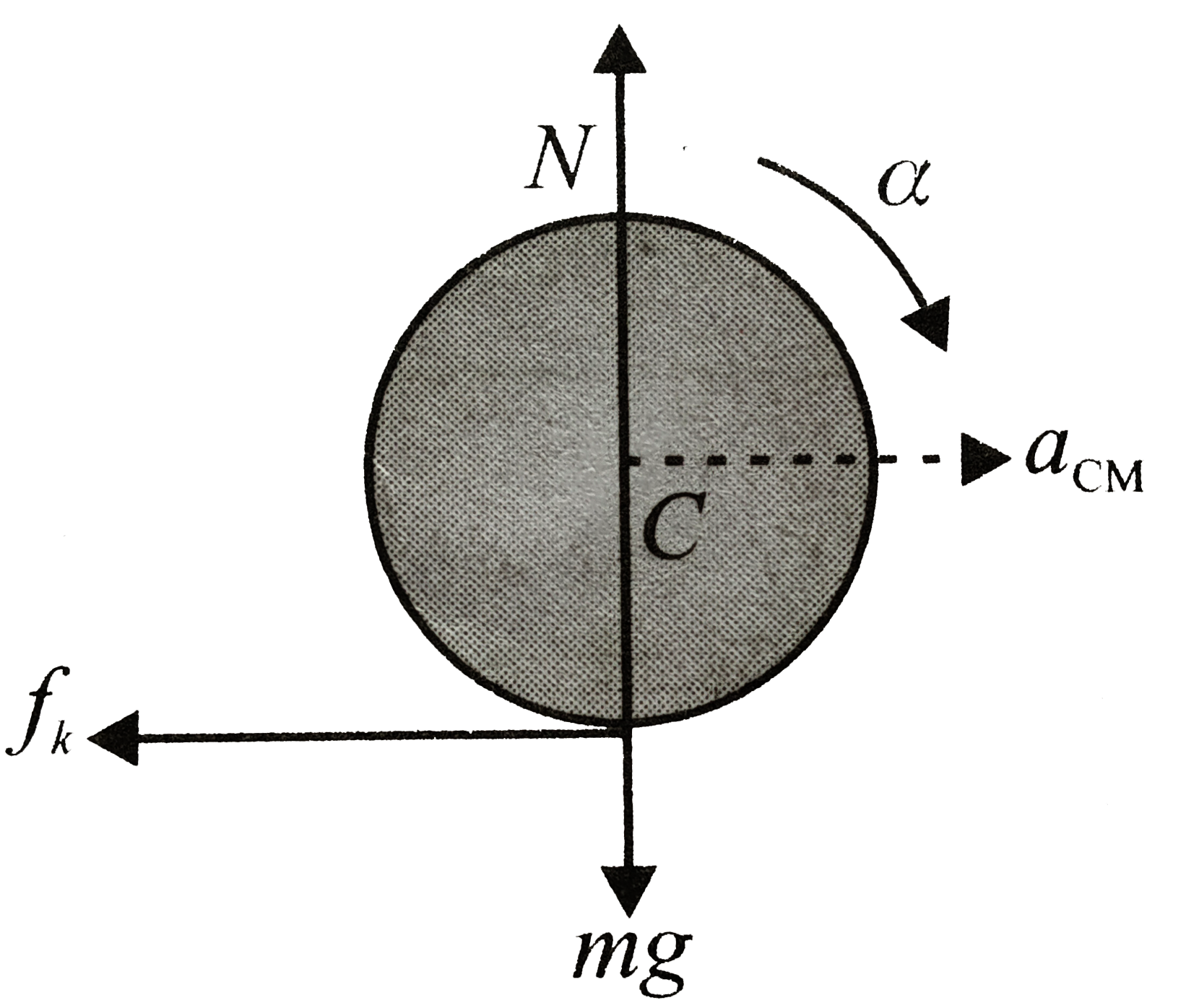
Method 1: Force/Torque Method: The forces acting on the ball are as shown in Fig. Let the acceleration of the centre of mass be $a_{C M}$ and its angular acceleration about the centre of mass axis be $α$ as shown in the figure.

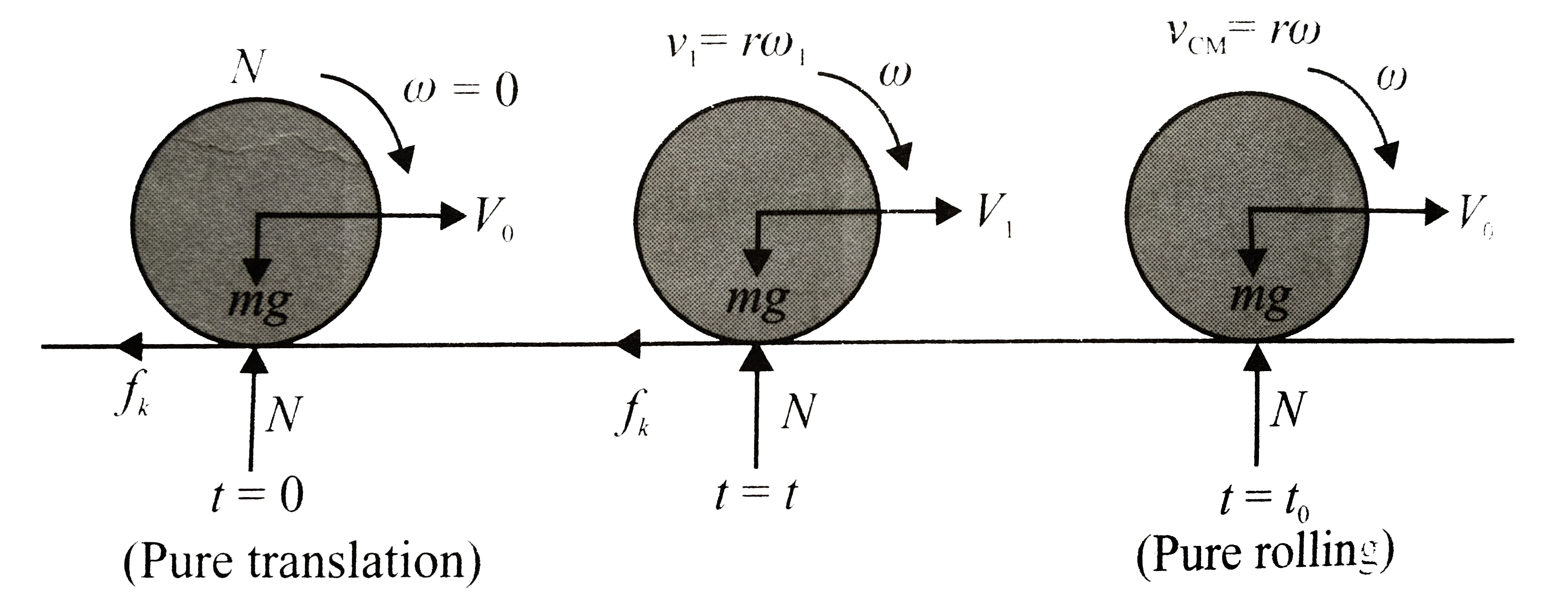
The following filgus represent the forces, accelerations and velocities of the ball in three different positions.

Force equations: $N - m g = 0$ (in the vertical direction)
$- f_{k} = m a_{C M}$ ( in the horizontal direction)
$\Rightarrow a_{C M} = - \frac{f_{k}}{m}$ ...........i
And from $τ_{C M} = I_{C M} α$
$\Rightarrow f_{k} r (\frac{2}{5} m r^{2}) α$
$\Rightarrow α ⎛ ⎝ \frac{f_{k} r}{\frac{2}{5} m r^{2}} ⎞ ⎠$ ..........ii
Let the velocity of the centre of mass be $v_{C M}$ and angular velocity about the centre of mass axis be $ω$ when rolling starts.
$v_{C M} + v_{0} + (\frac{- f_{k}}{m}) t$ (using $v = u + a t$ )...........iii
and $ω = 0 + ⎛ ⎝ \frac{f_{k} r}{\frac{2}{5} m r^{2}} ⎞ ⎠ t (ω = ω_{0} + a t)$ ............iv
also $v_{C M} = r ω$
Solving eqn iii, iv, and v for $v_{C M},$ we get
$v_{C M} = \frac{5}{7} v_{0}$
Method 2: Work Energy Theorem
Apply the work energy theorem for the translation and rotational components of the motion separately.
$\sum W_{force} = △ K_{translational}$
$\sum W_{torque} = △ K_{rotational}$

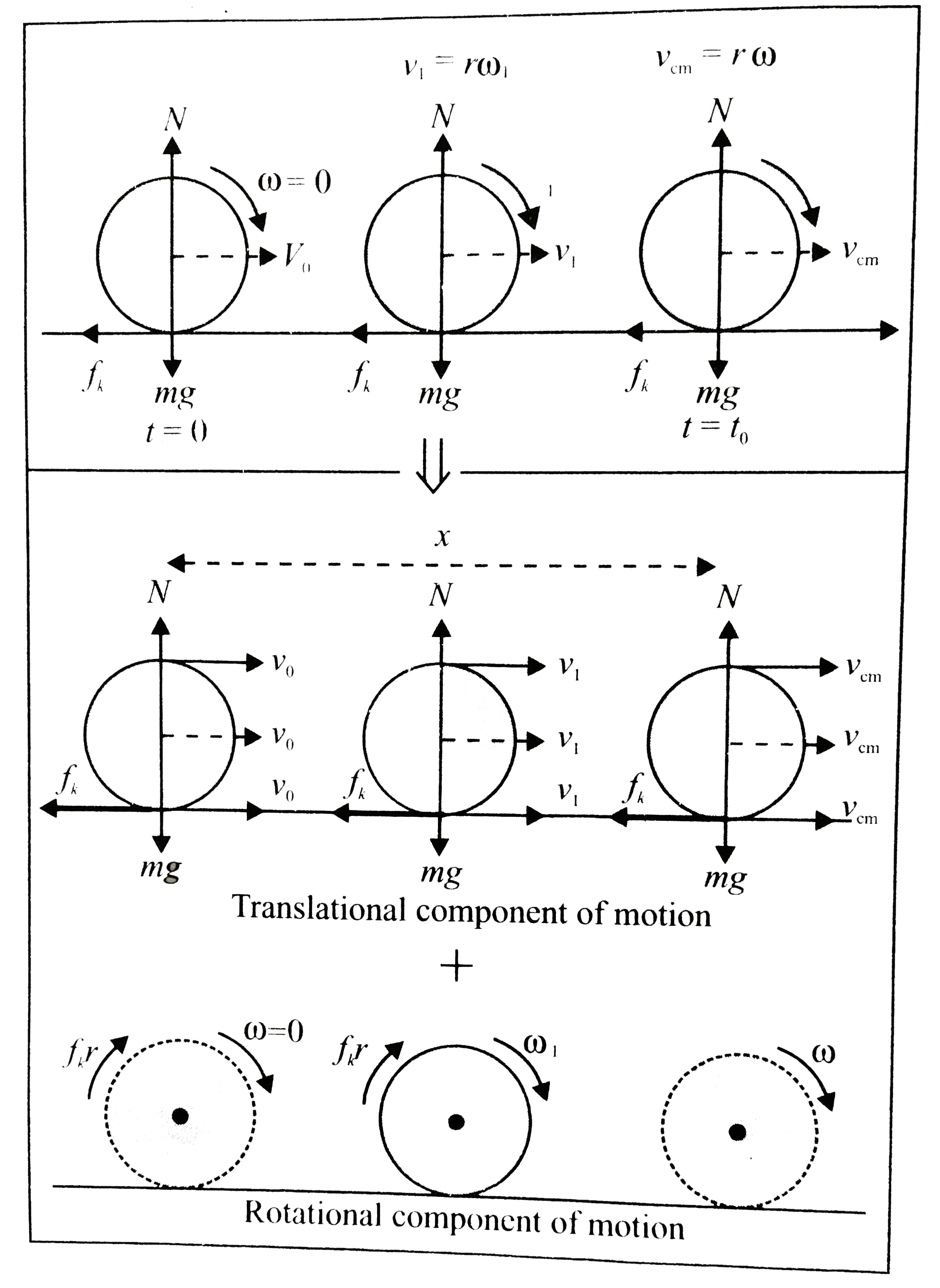
Mathematically $W_{f_{k}} + W_{N} + W_{m g} = {(K_{2} - K_{2})}_{translational}$
$\Rightarrow - f_{k} x + 0 + 0 = \frac{1}{2} m v^{2} - \frac{1}{2} m v_{0}^{2}$
$= - f_{k} (v_{a v} t) = \frac{1}{2} (v^{2} - v_{0}^{2}) [∵ x = v_{a v} t]$
$\Rightarrow - f_{k} (\frac{v + v_{0}}{2}) t = \frac{1}{2} m (v - v_{0}) (v + v_{0})$ ............i
in case of constant acceleration only $v - (a v) = \frac{v_{i} + v_{f}}{2}$
And for the rotational component of motion
$f_{k} r θ = \frac{1}{2} I_{C M} ω^{2} - 0$
$\to f_{k} r (ω_{a v} t) = \frac{1}{2} I_{C M} ω^{2}$
$\Rightarrow f_{k} r (\frac{0 + ω}{2}) t = \frac{1}{2} \times \frac{2}{5} m r^{2} \times ω^{2}$
[In case of constant angular acceleration $ω_{a v} = \frac{ω_{i} + ω_{f}}{2}$ ]
$\Rightarrow f_{k} r \frac{ω}{2} t = \frac{1}{2} \times \frac{2}{5} m r^{2} ω^{2}$ ..............ii
From eqn i and ii we get
$\frac{- \frac{f_{k} (v + v_{0})}{2} t}{f_{k} r \frac{ω}{2} t} = \frac{\frac{1}{2} m (v + v_{0}) (v - v_{0})}{\frac{1}{2} \times \frac{2}{5} m r^{2} ω^{2}}$
$\Rightarrow 1 = \frac{v - v_{0}}{\frac{2}{5} ω r}$
But $r ω = v,$
$- 1 = \frac{v - v_{0}}{\frac{2}{5} ω r}$
$\Rightarrow - \frac{2}{5} v = v - v_{0}$
$\Rightarrow v_{0} = v + \frac{2}{5} v = \frac{7}{5} v$
$\Rightarrow v = \frac{5}{7} v_{0}$
Method 3: By conservation of Angular Moentum

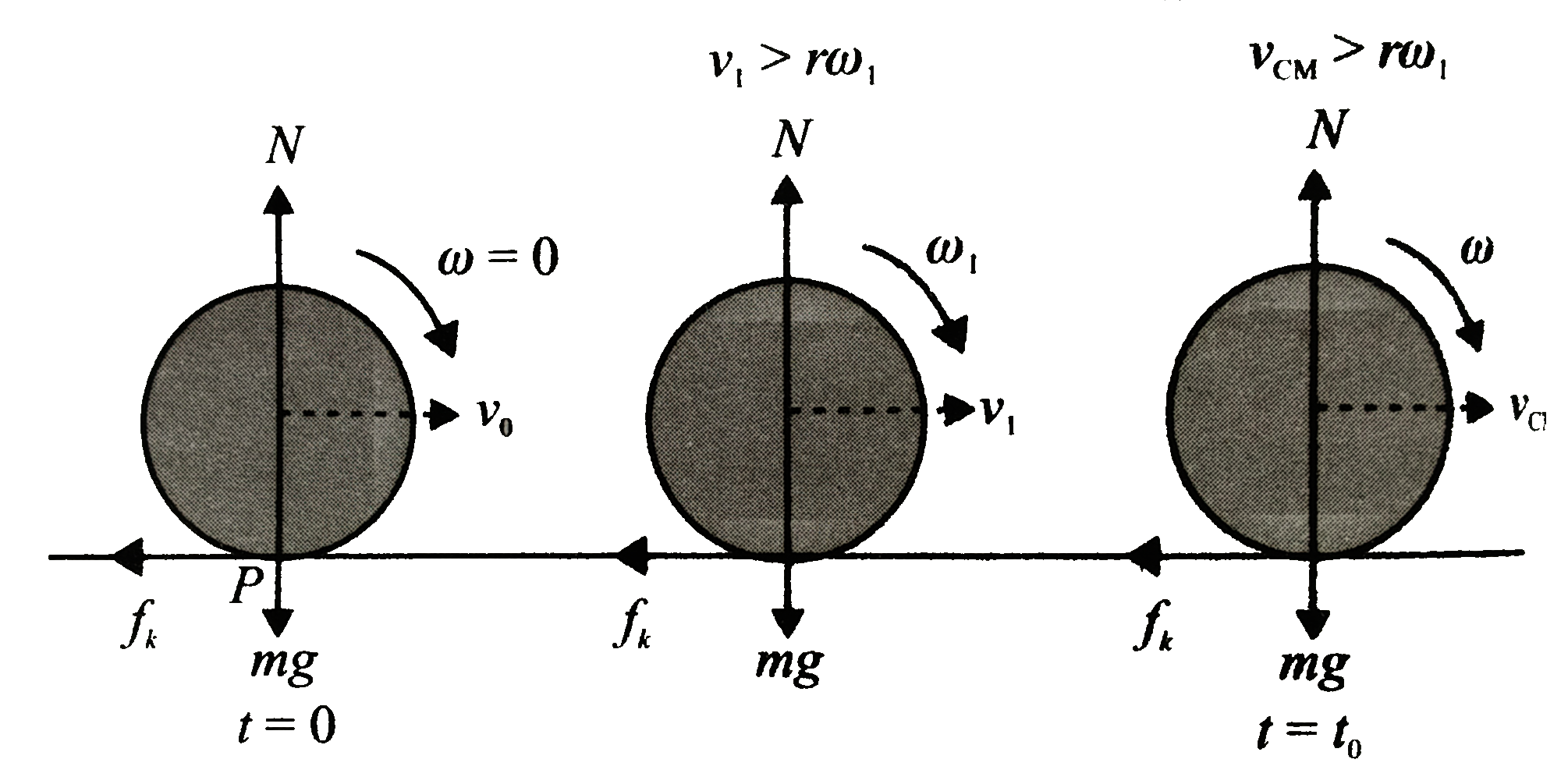
If $\to τ = 0 \frac{\to d L}{d t} = 0, L =$ constant
The torque acting on the ball for all its position, about point $P$ (a point on the ground as shown in figure. is zero. So the anguar momentum of the ball about poitn $P$ will remain constant.
$\Rightarrow m v_{0} r = I_{C M} ω + m v r$
$\Rightarrow m v_{0} r = \frac{2}{5} m r^{2} (\frac{v}{r}) + m v r (ω = \frac{v}{r})$
$\Rightarrow v_{0} = \frac{2}{5} v + v$
$\Rightarrow v = \frac{5}{7} v_{0}$

Updated on:21/07/2023