A ball with charge −50e is placed at the centre of a hollow spherical shell has a net charge of −50e. What is the charge on the shell's outer surface ?
−50e
zero
−100e
+100e
The correct Answer is:C
To solve the problem, we need to analyze the situation involving the charged ball and the hollow spherical shell. Here is the step-by-step solution:
Step 1: Understand the setup
We have a ball with a charge of −50e placed at the center of a hollow spherical shell. The shell itself has a net charge of −50e.
Step 2: Apply Gauss's Law
According to Gauss's Law, the electric field inside a conductor in electrostatic equilibrium is zero. This means that any excess charge on the shell will redistribute itself in such a way that the electric field inside the shell (and thus at the location of the charge) is zero.
Step 3: Determine the induced charge on the inner surface of the shell
The charge on the ball −50e will induce a charge of +50e on the inner surface of the shell. This is because the inner surface must have a charge that cancels the electric field due to the charge at the center to maintain zero electric field inside the conductor.
Step 4: Calculate the charge on the outer surface of the shell
The total charge on the shell is −50e. Since we have induced +50e on the inner surface, we can find the charge on the outer surface by using the equation:
Charge on outer surface=Total charge on shell−Charge on inner surface
Substituting the values:
Charge on outer surface=−50e−(+50e)=−50e−50e=−100e
Conclusion
The charge on the outer surface of the shell is −100e.
---
We have a ball with a charge of −50e placed at the center of a hollow spherical shell. The shell itself has a net charge of −50e.
According to Gauss's Law, the electric field inside a conductor in electrostatic equilibrium is zero. This means that any excess charge on the shell will redistribute itself in such a way that the electric field inside the shell (and thus at the location of the charge) is zero.
The charge on the ball −50e will induce a charge of +50e on the inner surface of the shell. This is because the inner surface must have a charge that cancels the electric field due to the charge at the center to maintain zero electric field inside the conductor.
The total charge on the shell is −50e. Since we have induced +50e on the inner surface, we can find the charge on the outer surface by using the equation:
The charge on the outer surface of the shell is −100e.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Both question (33) and (34) refer to the system of charges as shown in the figure. A spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting material. A point charge +Q is placed at the centre of the spherical shell and a total charge -q is placed on the shell.
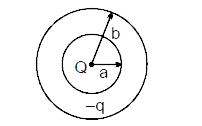
Assume that the electrostatic potential is zero at an infinite distance from the spherical shell. The electrostatic potential at a distance R(a<R<b) from the centre of the shell is
View SolutionTwo concentric conducting shells A and B are of radii R and 2R. A charge +q is placed at the centre of the shells. Shell B is earthed and a charge q is given to shell A. Find the charge on outer surface of A and B.
View Solution
Knowledge Check
A charge Q is placed at the centre of a spherical conducting shell. Choose the correct option.
AOnly −Q will appear on its inner surfaceBOnly +Q will appear on its outer surfaceCA charge −Q will appear on its surface and +Q on its outer surfaceDA charge +Q will appear on its inner surface and −Q on its outer surfaceA point charge is kept at the centre of a metallic insulated spherical shell. Then
AElectric field out side the sphere is zeroBelectric field inside the sphere is zeroCNet induced charge on the sphere is zeroDElectric potential inside the sphere is zeroShown in the figure a spherical shell with an inner radius 'a' and an outer radius 'b' is made of conducting metarial. A charge +Q is placed at the centre of the spherical shell and a total charge -q s placed on the shell. Charge -q is districuted on the surfaces as :
 A−Q on the inner surface, −q on outer surfaceB−Q on the inner surface, −q+Q on the outer surfaceC+Q on the inner surface, −q−Q on the outer surfaceDThe charge −q is spread uniformly between the inner and outer surface
A−Q on the inner surface, −q on outer surfaceB−Q on the inner surface, −q+Q on the outer surfaceC+Q on the inner surface, −q−Q on the outer surfaceDThe charge −q is spread uniformly between the inner and outer surface
A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA metalic spherical shell has an inner radius R1and outer radius R2 . A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface and (ii) the outer surface?
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionBoth question a and b refer to the sustem of charges as shown in the figure. A spherical shell of conducting material. A point charge +Q is place at the centre of the spherical shell and a total charge −q is placed on the shell. A Charge −q id distributed on the surfaces as
 .
.
(b) Assume that the elctrostatic potential is zero at an infinite distance from the spherical shell . The electrostatic potential at a distance R(a<R<b) from the centre of the shell is .
View SolutionA conducting sphere that carries a total charge of -3q is placed at the centre of a conducting spherical shell that carries a total charged of +5q. The conductors are in electrostatic equilibrium. The charges on the inner and outer surfaces of the shell are respectively.

View Solution
