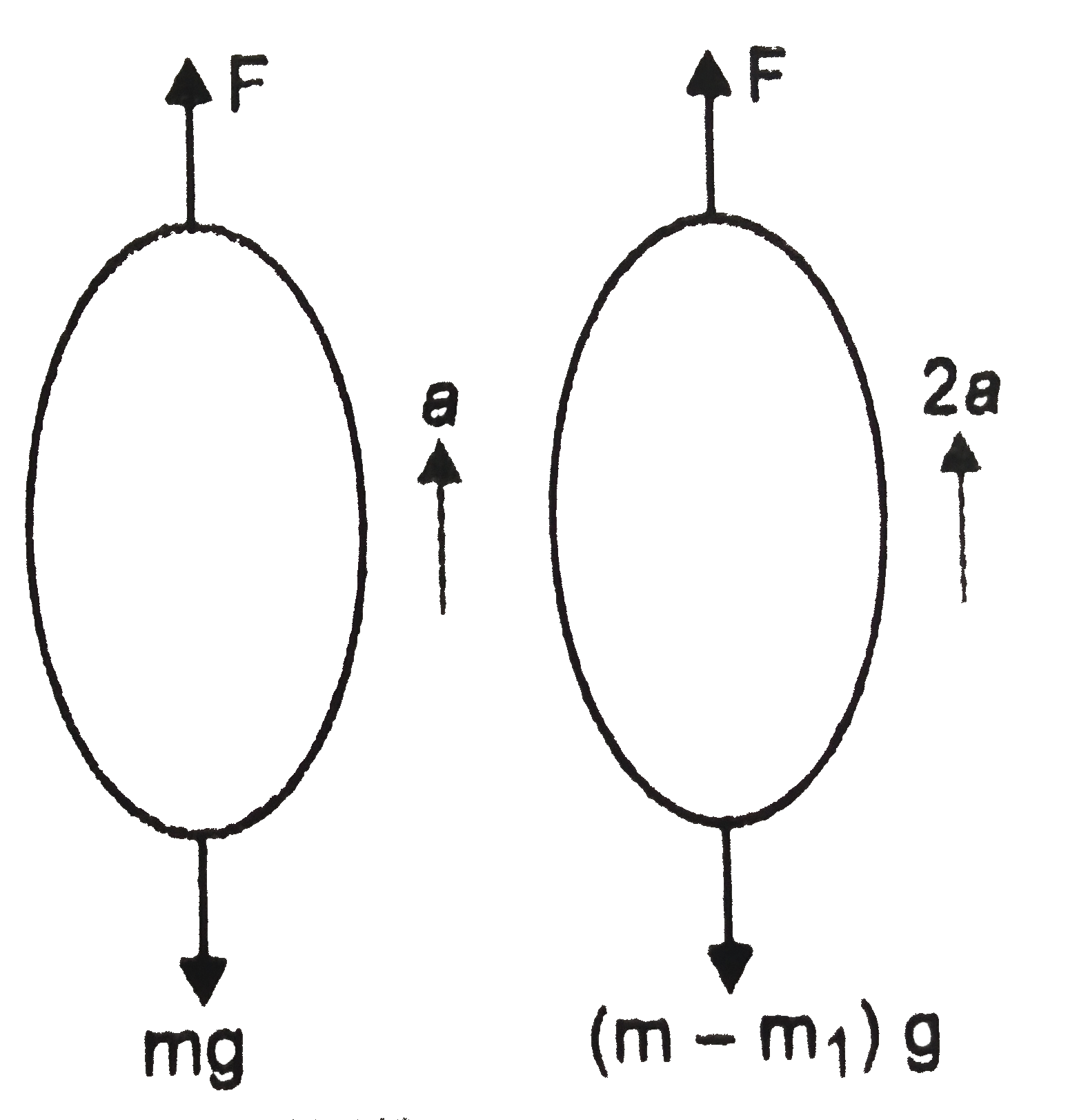
A balloon of mass m is rising up with an acceleration a.

A

The upthrust on the balloon is $m (g + a)$ .

B

The upthrust on the balloon is ma.

C

$m a / (2 a + g)$ mass must be detached in order to double its acceleration.

D

m/2 mass must be detached in order to double its acceleration.

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A, C

To solve the problem of a balloon of mass $m$ rising with an acceleration $a$ , we will analyze the forces acting on the balloon and apply Newton's second law of motion.
1. Identify the Forces Acting on the Balloon:
- The weight of the balloon, $W$ , acting downwards is given by:
$W = m g$
- The buoyant force (upthrust) acting upwards, which we denote as $U$ .
2. Apply Newton's Second Law:
- According to Newton's second law, the net force acting on the balloon is equal to the mass of the balloon multiplied by its acceleration:
$F_{net} = m a$
- The net force acting on the balloon can also be expressed as the difference between the buoyant force and the weight:
$F_{net} = U - m g$
3. Set Up the Equation:
- Equating the two expressions for net force, we have:
$U - m g = m a$
- Rearranging this gives:
$U = m g + m a$
4. Determine the Buoyant Force:
- From the equation derived, we can express the buoyant force as:
$U = m (g + a)$
- This indicates that the buoyant force must be equal to the weight of the balloon plus the force required to accelerate it upwards.
5. Consider Doubling the Acceleration:
- If we want to double the acceleration to $2 a$ , we need to find the new mass of the balloon after detaching some mass $m^{'}$ .
- The new mass of the balloon will be $m - m^{'}$ , and the new equation for the buoyant force will be:
$U = (m - m^{'}) g + (m - m^{'}) \cdot 2 a$
6. Set Up the New Equation:
- Setting the new buoyant force equal to the new weight gives:
$U = (m - m^{'}) g + (m - m^{'}) \cdot 2 a$
- Since the buoyant force remains the same, we can equate it to the original buoyant force:
$m (g + a) = (m - m^{'}) g + (m - m^{'}) \cdot 2 a$
7. Solve for $m^{'}$ :
- Expanding and rearranging the equation will help us isolate $m^{'}$ :
$m g + m a = m g - m^{'} g + 2 m a - 2 m^{'} a$
- Simplifying this leads to:
$m a + m^{'} g = 2 m a - 2 m^{'} a$
- Collecting terms involving $m^{'}$ gives:
$m^{'} (g + 2 a) = m a$
- Finally, solving for $m^{'}$ gives:
$m^{'} = \frac{m a}{g + 2 a}$
Conclusion:
Thus, the mass that needs to be detached to double the acceleration of the balloon is given by:
$m^{'} = \frac{m a}{g + 2 a}$

|

Updated on:18/9/2024

Class 12 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A balloon os mass 2 KG is rising up with an acceleration of $4 \frac{m}{s^{2}}$ . The upward force acting on the balloon is $(g = 10 m s^{- 2}$
A0.8 kgf
B2.8 kgf
C2.4 kgf
D2.0 kgf
Question 2 - Select One
A balloon of mass 10 kf is raising up with an acceleration of $20 m s^{- 2}$ . If a mass of 4 kg is removed from the balloon its acceleration becomes ( take, $g = 10 m s^{- 2}$ )
A $40 m s^{- 2}$
B $20 m s^{- 2}$
C $30 m s^{- 2}$
D $12 m s^{- 2}$
Question 3 - Select One
A balloon of mass $M$ descends with an acceleration $a_{0}$ . The mass that must be thrown out in order to give the balloon an equal upwards acceleration will be
A $\frac{M a_{0}}{g}$
B $\frac{2 M a_{0}}{g}$
C $\frac{2 M a_{0}}{g + a_{0}}$
D $\frac{M (g + a_{0})}{a_{0}}$

RESNICK AND HALLIDAY-FORCE AND MOTION - I -PRACTICE QUESTIONS (More than One Correct Choice Type)

Home
Ask Doubt
Profile