A bar of mass m1 is placed on a plank of mass m2, which rests on a smooth horizontal plane (Fig. 6-24a). The coefficient of friction between the surfaces of the bar and the plank is equal to μ. The plank is subjected to the horizontal force F depending on time t as F= at (a is a constant).

A bar kept on a plank which is subjected to a horizontal force.
Find (a) the moment of time t0 at which the plank starts sliding from under the bar and (b) the acceleration of the bar a1 and that of plank a2 during motion.
This problem is similar to problems that we have already solved. Here as the force F grows, so does the static friction force fs. However, the friction force f has the limiting value flimit=μm1g. Unless this value is reached, both bodies move together with equal accelerations. But as soon as the force f reaches this limit, mass m2 starts sliding under mass m1.
Calculations: Let us make free-body diagram as shown in Fig. 6-24b.

Writing Newton.s second law for the plank and the bar, having taken the positive direction of the x axis as shown in Fig. 6-24b.
f=m1a1,F−f=m2a2
Acceleration of m, must be always greater than or equal to the acceleration of m1 that is a2≥a1 where the sign .=. corresponds to the moment t=t0. Hence, when f=μm1g, then sliding begins. Putting f=μm1g in Eq. 6-28, we get
t0=(m1+m2)μga
When t≤t0, then
a1=a2=at(m1+m2)
and when t≥t0. then they separate. Only force acting on m1 is friction, whose value is constant.
Thus, a1=μg= constant
Now m2 is experiencing force F and constant friction thus, at−μm1g=m2a2
Solving we get
a2=(at−μm1g)m2
Note: You may have been tempted to think that when external force F(=at) is equal to μm1g, slipping will begin. You can check that at this instant t2 they are moving with same acceleration.
at2=μm1g
t2=μm1ga
Let.s find force of friction between the blocks at this instant.
μm1g−f=m2a
f=m1a
Solving for friction
f=μm1g(1+m2m1)
Since friction is less than the limiting value, slipping has not yet begun.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS5videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS33videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)3videos
GAUSS' LAW
Similar Questions
A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together
 View Solution
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g - Question 2 - Select One
A block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
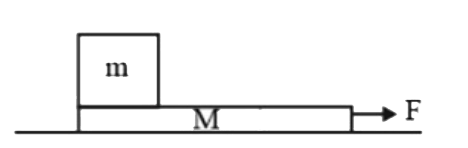 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 N - Question 3 - Select One
Two bars of masses m1 and m2 connected by a non−deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to μ. What minimum constant force has to be appled in the horizontal direction to the bar of mass m1 in order to shift the other bar?
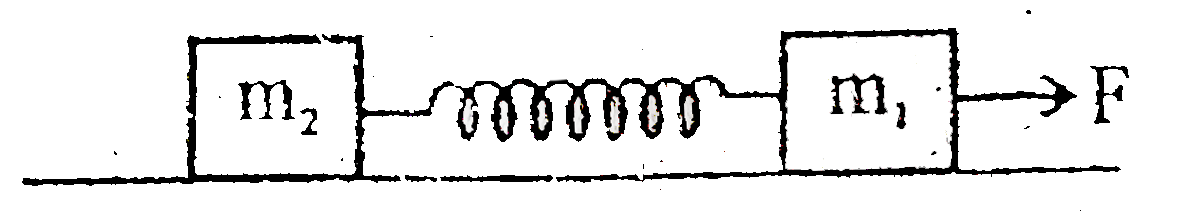 A(m1+m22)μgB(m2+m12)μgC(m1−m22)μgD(2m2+m12)μg
A(m1+m22)μgB(m2+m12)μgC(m1−m22)μgD(2m2+m12)μg
A bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
 View Solution
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 View Solution
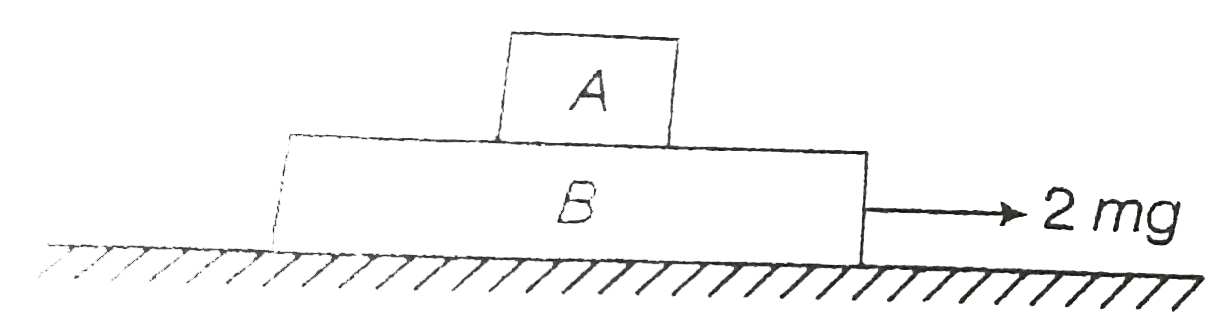
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizo-ntal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are:
 View Solution
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 View Solution
View SolutionBlock of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
 View Solution
View Solution

