A baseball is hit into the air at an initial speed of 36.6 m/s and an angle of 50.0∘ above the horizontal. At the same time, the center fielder starts running away from the batter, and he catches the ball 0.914 m above the level at which it was hit. If the center fielder is initially 1.10×102m from home plate, what must be his average speed?
3.5 m/s
5.0 m/s
4.2 m/s
6.9 m/s
The correct Answer is:C
To solve the problem, we will break it down into several steps:
Step 1: Determine the initial velocity components of the baseball.
The initial speed of the baseball is given as v0=36.6m/s at an angle of θ=50∘.
- The horizontal component of the initial velocity v0x is given by:
v0x=v0cos(θ)=36.6cos(50∘)
- The vertical component of the initial velocity v0y is given by:
v0y=v0sin(θ)=36.6sin(50∘)
Calculating these values:
v0x≈36.6×0.6428≈23.5m/s
v0y≈36.6×0.7660≈28.0m/s
Step 2: Use the vertical motion equation to find the time of flight until the ball reaches a height of 0.914 m.
Using the second equation of motion:
h=v0yt−12gt2
where h=0.914m and g=9.8m/s2.
Substituting the values:
0.914=28.0t−4.9t2
Rearranging gives:
4.9t2−28.0t+0.914=0
Step 3: Solve the quadratic equation for time t.
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=4.9, b=−28.0, and c=0.914.
Calculating the discriminant:
D=b2−4ac=(−28.0)2−4×4.9×0.914
D=784−17.912=766.088
Now substituting back into the quadratic formula:
t=28.0±√766.0882×4.9
Calculating √766.088≈27.7:
t=28.0±27.79.8
Calculating the two possible times:
1. t1=55.79.8≈5.68s (valid)
2. t2=0.39.8≈0.03s (not valid)
Step 4: Calculate the horizontal distance traveled by the baseball.
Using the horizontal motion:
d=v0x⋅t
Substituting the values:
d=23.5×5.68≈133.48m
Step 5: Determine the distance the center fielder must run.
The center fielder starts at a distance of 110m from home plate:
Distance to run=d−110=133.48−110=23.48m
Step 6: Calculate the average speed of the center fielder.
The average speed v is given by:
v=DistanceTime=23.485.68≈4.13m/s
Final Answer:
The average speed of the center fielder must be approximately 4.13m/s.
---
The initial speed of the baseball is given as v0=36.6m/s at an angle of θ=50∘.
v0x=v0cos(θ)=36.6cos(50∘)
- The vertical component of the initial velocity v0y is given by:
v0y=v0sin(θ)=36.6sin(50∘)
v0x≈36.6×0.6428≈23.5m/s
v0y≈36.6×0.7660≈28.0m/s
Using the second equation of motion:
h=v0yt−12gt2
where h=0.914m and g=9.8m/s2.
0.914=28.0t−4.9t2
Rearranging gives:
4.9t2−28.0t+0.914=0
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=4.9, b=−28.0, and c=0.914.
D=b2−4ac=(−28.0)2−4×4.9×0.914
D=784−17.912=766.088
t=28.0±√766.0882×4.9
Calculating √766.088≈27.7:
t=28.0±27.79.8
Calculating the two possible times:
1. t1=55.79.8≈5.68s (valid)
2. t2=0.39.8≈0.03s (not valid)
Using the horizontal motion:
d=v0x⋅t
Substituting the values:
d=23.5×5.68≈133.48m
The center fielder starts at a distance of 110m from home plate:
Distance to run=d−110=133.48−110=23.48m
The average speed v is given by:
v=DistanceTime=23.485.68≈4.13m/s
The average speed of the center fielder must be approximately 4.13m/s.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A ball is thrown from a field with a speed of 12.0 m/s at an angle of 450 with the horizontal. At what distance will it hit the field again ? Take g=10.0ms2
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View Solution
Knowledge Check
- Question 1 - Select One
A paricle is projected from a point with initial speed of 10m/sec at an angle of 37∘ with the horizontal. At the same instant a fly starts on the same path of particle with constant speed of 10m/s Then :
Atime taken by fly to complete whole path is less then time taken by particleBacceleration of fly is zeroCaverage velocity of both are same for whole journeyDNone of these - Question 2 - Select One
An effective tactic in tennis, when your opponent is near the net, consists of lofting the ball over his head, forcing him to move quickly away from the net (see figure). Suppose that you loft the ball with an initial speed of 15.0 m/s, at an angle of 50.0∘ above the horizontal. At this instant your opponent is 10.0 m away from the ball. He begins moving away from you 0.30 s later, hoping to reach the ball and hit it back at the moment that it is 2.10 m above its launch point. With what minimum average speed must he move? (Ignore the fact that he can stretch, so that his racket can reach the ball before he does.)
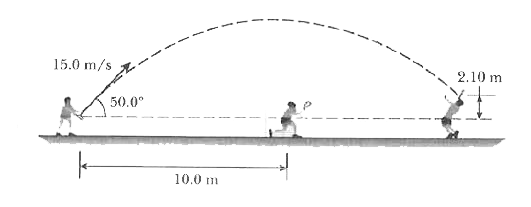 A4.98 m/sB5.79 m/sC5.14 m/sD9.64 m/s
A4.98 m/sB5.79 m/sC5.14 m/sD9.64 m/s - Question 3 - Select One
The coach throws a baseball to a player with an initial speed at 20ms−1 at an angle of 45∘ with the horizontal.At the moment the ball is thrown, the player is 50m from coach.The speed and the direction that the player has to run to catch the ball at the same height at which it was released in ms−1 is
A5√2away from coachB5√2 towards from coachC√25towards the coachD√25away from the coach
A ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionThe coach throws a baseball to a player with an initial speed of 20m/s at an angle of 45∘ with the horizontal. At the moment the ball is thrown, the player is 50 m from the coach. At what speed and in what direction must the player run to catch the ball at the same height at which it was released? (g=10m/s2).
View SolutionA soccer ball is kicked from the ground with an initial speed of 21.3 m/s at an upward angle of 45∘. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to meet the ball just before it hits the ground?
View SolutionA ball is projected from ground with a speed of 20ms−1 at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height of
View SolutionA satellite of mass 5000kg is projected in space with an intial speed of 400m/s making an angle of 30∘ with the radial direaction from a distance 3.6×107m away from the center of the earth.
The angular momentum of satellite :View Solution

