A beaker exactly full of water has an ice piece floating on it. As the cube melts what happens to the water level if (a) the cube contains an air bubble, (b) the cube contains (i) a lead piece and (ii) a cork piece.
If Mg of ice containing an air bubble is floating in water,
Mg=VDσWg
i.e., VD=(M/σw)
[as air bubble encloses air which is weightless]
Now when Mg ice melts, water formed will be Mg and its will occupy volume VF=(M/σW). As the volume of water formed by melting of ice is equal to the volume of water displaced by the floating ice, the level of water in the beaker will remain unchanged.
b. Let the mass of ice be Mg and that off embedded piece m, then for floating
Weight = upthrust, i.e., (Mm)g=VDσwg
So the volume of water displaced by the system when floating
VD=Mσw+mσW........i
Now when ice melts, water fomed will be Mg and so the water displaced by it will be equal to its own volume.
V2=(m/ρpb) [as ρ=m/V)]
So finally total volume occupied by water formed by melting of ice and lead piece
V1+V2=MσW+mρpb........ii
Now as ρpb>σw, this volume will be lesser than initial water displaced by the floating system Eq. i so the level of water in beaker will go down as the ice melts if the ice contains a sinking impurity.
ii. If the ice initially contains a cork piecce, then as ρrock<σW, the cork will float on water when ice melts. so the water displaced by the floating cork piece will be
mg=V′2σWg
⇒V′2=m/σW
[and not its own volume (m/ρrock)]
So in this calse, water formed by melting of Mg of ice and water displaced by floating cork.
V1+V′2=MsimgaW+mσW.............iii
and as this is same as initially volume displaced by the floating system (Eq. i), the level of water in the beaker will remain unchanged.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.2
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A glass of water has an ice cube floating in water. The water level just touches the rim of the glass. Will the water overflow when the ice melts?
View SolutionAn ice block with a cork piece embedded inside floats in water.What will happen to the level of water when ice melts ?
View SolutionA piece of ice is floating in a beaker containing thick sugar solution of water. As the ice melts, the total level of he liquid
View SolutionA piece of ice is floating in a glass vessel filled with water. Then prove that level of water in the vessel remains unchanged after melting of ice.
View SolutionA piece of ice is in the form of a cube melts so that the percentage error in the edge of cube is a , then find the percentage error in its volume.
View SolutionA boat containing some piece of material is floating in a pond. What will happen to the level of water in the pond if on unloading the pieces in the pond, the piece (a) floats, (b) sinks?
View SolutionA piece of ice is floating in a glass vessel filled with water. How will the level of water in the vessel change when the ice melts ?
View SolutionAn ice cube is floating in water above which a layer of a fighter oil is poured. As the ice melts completely, the level If water surface (or interface) and upper level of oil will
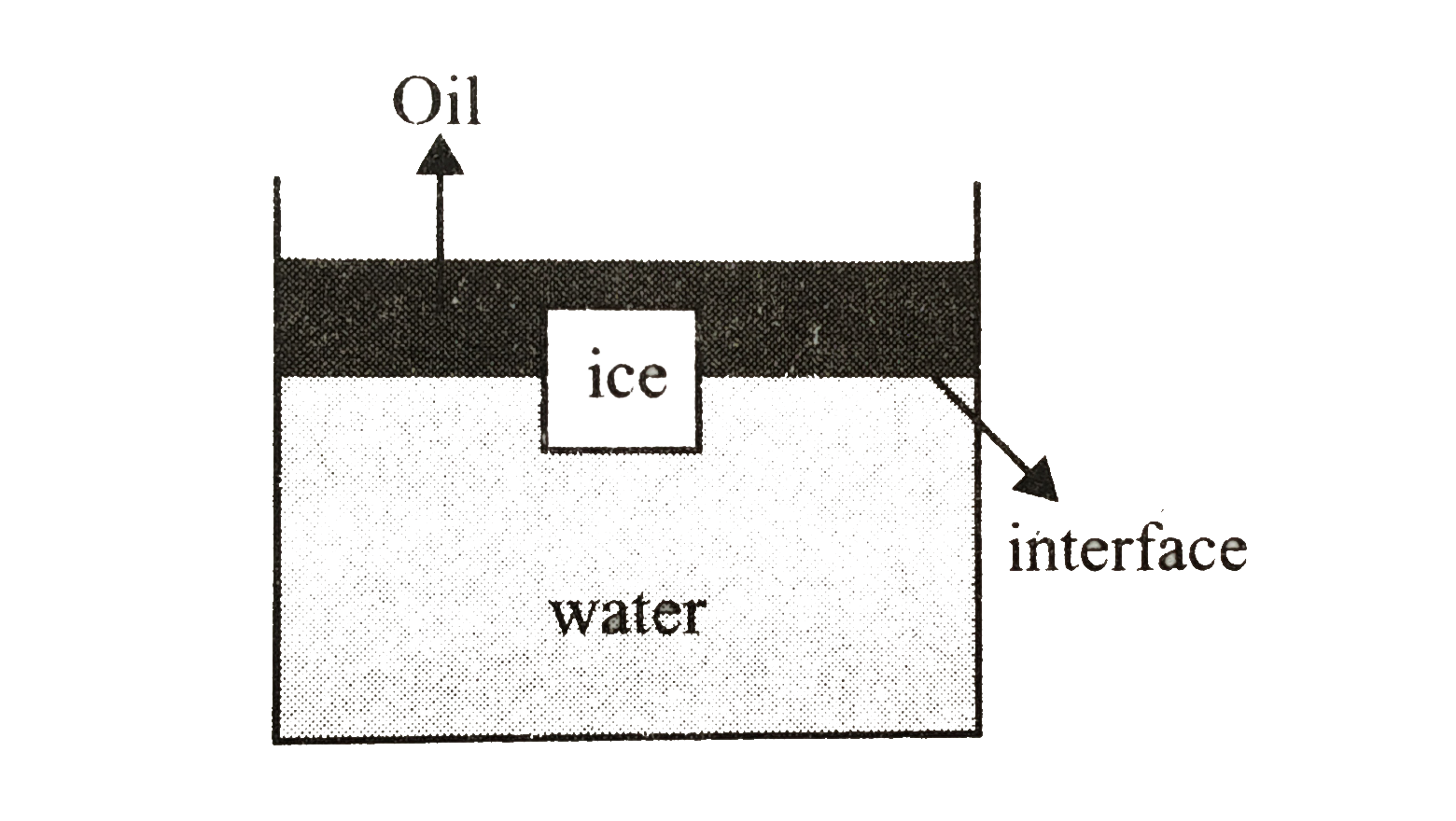
View SolutionA piece of ice is floating in a vessel containing water and inside the ice is a bubble of air. What will be the effect on the level of water, when the ice melts?
View SolutionStatement-1: An ice cube is floating in water in a vessel at 0∘C when ice cube melts level of water in the vessel remain same.
Statement-2: Volume of melted ice is same as volume of water displaced by ice.
View Solution
