A beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
To solve the problem of finding the magnitude of the smallest magnetic field that can prevent a beam of charged particles from striking a plate, we can follow these steps:
Step 1: Understand the relationship between the radius of the path, magnetic field, and kinetic energy.
The radius R of the circular path of a charged particle moving in a magnetic field is given by the formula:
R=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
Step 2: Relate kinetic energy to velocity.
The kinetic energy Ek of the particle is given by:
Ek=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2Ekm
Step 3: Substitute the expression for velocity into the radius formula.
Substituting v into the radius formula gives:
R=m√2EkmqB=√2mEkqB
Step 4: Rearrange to find the magnetic field B.
Rearranging the formula to solve for B:
B=√2mEkqR
Step 5: Calculate the charge of the particles.
For charged particles, we can use the elementary charge q=1.6×10−19C.
Step 6: Substitute the known values.
We have:
- Kinetic energy Ek=103eV=103×1.6×10−19J=1.6×10−16J
- Distance R=10−2m
- Masses m1=8×10−27kg and m2=1.6×10−26kg
Step 7: Calculate B for both masses.
We will calculate B using the larger mass m2=1.6×10−26kg:
B=√2×(1.6×10−26)×(1.6×10−16)(1.6×10−19)×(10−2)
Step 8: Perform the calculations.
Calculating the numerator:
√2×(1.6×10−26)×(1.6×10−16)=√5.12×10−42=7.15×10−21
Calculating the denominator:
(1.6×10−19)×(10−2)=1.6×10−21
Thus,
B=7.15×10−211.6×10−21≈4.47T
Step 9: Conclusion
The magnitude of the smallest magnetic field required to prevent the beam from striking the plate is approximately 4.47T.
The radius R of the circular path of a charged particle moving in a magnetic field is given by the formula:
R=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
The kinetic energy Ek of the particle is given by:
Ek=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2Ekm
Substituting v into the radius formula gives:
R=m√2EkmqB=√2mEkqB
Rearranging the formula to solve for B:
B=√2mEkqR
For charged particles, we can use the elementary charge q=1.6×10−19C.
We have:
- Kinetic energy Ek=103eV=103×1.6×10−19J=1.6×10−16J
- Distance R=10−2m
- Masses m1=8×10−27kg and m2=1.6×10−26kg
We will calculate B using the larger mass m2=1.6×10−26kg:
B=√2×(1.6×10−26)×(1.6×10−16)(1.6×10−19)×(10−2)
Calculating the numerator:
√2×(1.6×10−26)×(1.6×10−16)=√5.12×10−42=7.15×10−21
Calculating the denominator:
(1.6×10−19)×(10−2)=1.6×10−21
Thus,
B=7.15×10−211.6×10−21≈4.47T
The magnitude of the smallest magnetic field required to prevent the beam from striking the plate is approximately 4.47T.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example25videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
Calculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View SolutionA proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
View SolutionA beam of electrons whose kinetic energy is K emerges from a thin-foil "window" at end of an accelerator tube. A metal plate at distance d from this window is perpendicular to the direction of the emerging beam. (a) Show that we can prevent the beam from hitting the plate if we apply a uniform magnetic field such that
B≥√2mKe2d2
in which m and e are the electrons mass and charge
(b) How should →B be oriented?
 View Solution
View SolutionA charged particle having charge 10−6 C and mass of 10−10 kg is fired from the middle of the plate making an angle 30∘ with plane of the plate. Length of the plate is 0.17m and it is separated by 0.1m. Electric field E=10−3NC is present between the plates. Just outside the plates magnetic field is present. Find the velocity of projection of charged particle and magnitude of the magnetic field perpendicular to the plane of the figure, if it has to graze the plate at C and A parallel to the surface of the plate. (Neglect gravity)
 View Solution
View SolutionWhat will be the escape speed from a planet of mass 6×1016 kg and radius 3.6×104 m ?
View SolutionA charged particle having a mass of 1.6×10−26kg comes out of accelerator tube with kinetic energy 2×103eV . Calculate the smallest magnitude of the magnetic field that should be applied in vertically downwards direction to just prevent the charged particle from colliding the plate (Assume charge on particle = charge of the proton)
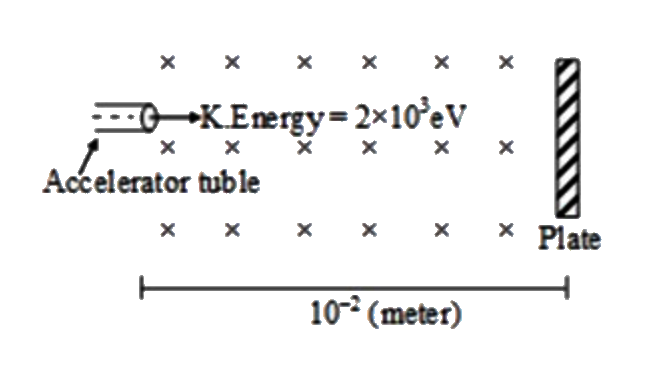 View Solution
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
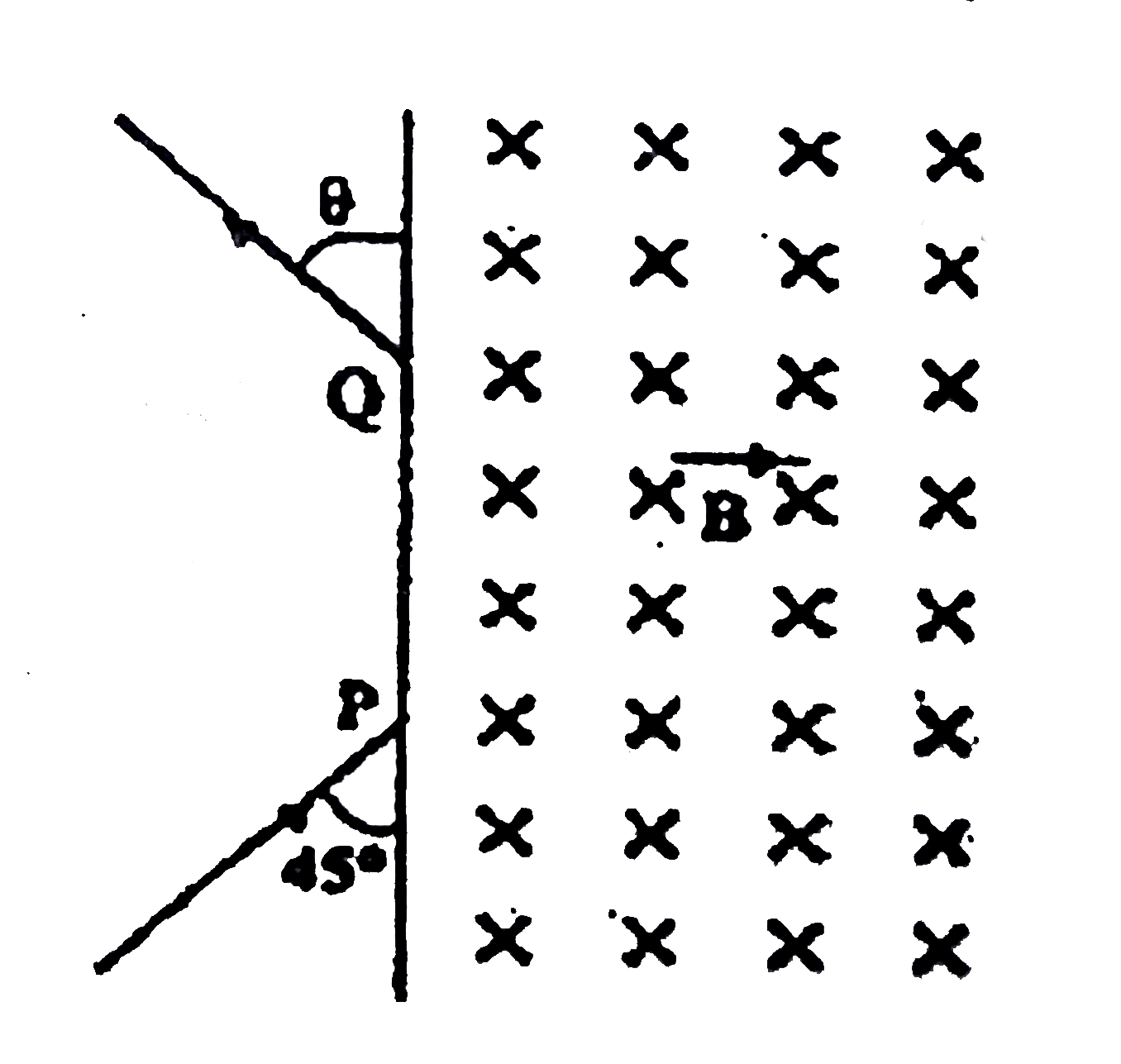 View Solution
View SolutionA planet has a mass of 2.4×1026 kg with a diameter of 3×108 m. What will be the acceleration due to gravity on that planet ?
View SolutionProtons having kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field so that it just misses a plane target kept at a distance I in front of the accelerator. Find the magnetic field.
View Solution

