A beam of fast moving alpha particles were directed towards a thin film of gold. The parts A',B' and C' of the transmitted and refected beams correcponding ro the incident parts A,B and C of the beam, are shown in the adjoining diagram. The number of alpha particles in

B' will be minimum and in C' maximum
A' will be maximum and in B' minimum
A' will be minimum and in B' maximum
C' will be minimum and in B' maximum
The correct Answer is:B
Because atom is hollow and whole mass of atom is concentrated in a small centre called nuclues.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Bohr'S Hydrogen Model
90 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Atomic Spectrum
53 Videos
- ALTERNATING CURRENTBOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Section D - Chapter End Test
30 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A beam of α - particle is incident on a gold foil . Corresponding to the incident beams A , B and C , the emergent beams A' , B' and C' . The transmission and deflection of α - particles through the foil take place such that

View Solution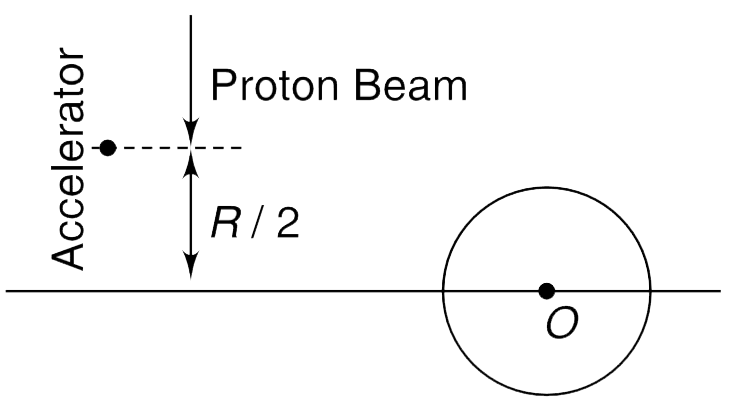
A proton accelerator produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as mP and the charge on it as e.
(a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere.
View Solution
Knowledge Check
A beam of mixture of α particle and protons are accelerted through same potential difference before entering into the magnetic field of strength B. if r1=5 cm then r2 is
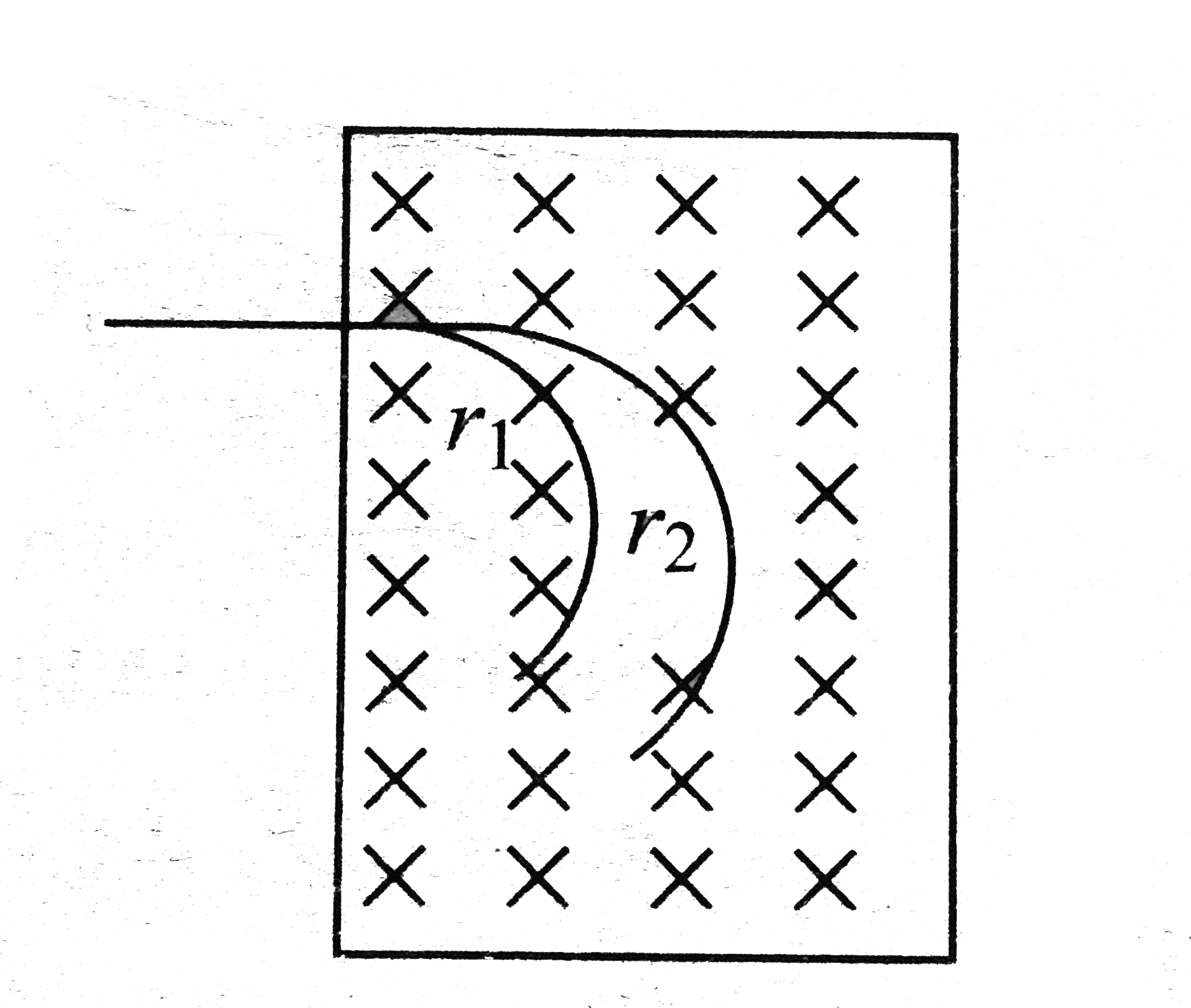 A5cmB5√2cmC10√2cmD20cm
A5cmB5√2cmC10√2cmD20cm
Answer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of -particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(b) Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α -particles by a thin foil?
View SolutionA parallel beam, of light of wavelength 100 nm passed through a sample of atomic hydrogen gas in ground state.
(a) Assume that when a phton supplies some of its energy to a hydrogen atom, the rest of the energy appears an another photon moving in the same direction as the incident photon. Neglecting the light emitted by the excited hydrogen atoms in the direction of the incident beam, what wavelengths may be observed in the transmitted beam?
(b) A radition detector is placed near the gas to detect radiation coming perpendicular to the incident beam. Find the wavelength of radiation that may be detected by the detector.
View SolutionAnswer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of -particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(b) Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α -particles by a thin foil?
View SolutionHow much energy is released when a 238U nucleus decays by emitting (a) an alpha particle and (b) a sequence of neutron, proton, neutron, proton? (c) Convince yourself both by reasoned argument and by direct calculation that the difference between these two numbers is just the total binding energy of the alpha particle. (d) Find that binding energy. Some needed atomic and particle masses are
View SolutionA beam of equally charged particles after being accelerated through a voltage V enters into a magnetic field B as shown in Fig. 1.31. It is found that all the particles hit the plate between C and D. Find the ratio between the masses of the heaviest and lightest particles of the beam.

View SolutionA narrow beam of alpha particles with kinetic energy 1.0MeV falls normally on a platinum foil 1.0μ thick. The scattered particles are observed at an angle of 60∘ to the incident beam direction by means of a counter with a circular inlet area 1.0cm2 located at the distacne 10cmfrom the scattering section of the foil. What fraction of scattered alpha particles reaches the counter inlet?
View SolutionA narrow beam of alpha particles with kinetic energy T==0.50MeV falls normally on a golden foil whose t=mass of thickness is ρd=1.5mg/cm2 The beam intensity is I0=5.0.105 particles per second. Find the number of alpha particles scattered by the foil during the time interval τ=30 m in into the angular interval:
(a) 59−61∘ , (b) over θ0=60∘.
View Solution
