A beam of light of two wavelengths 6500Å and 5200Å, is used to obtain interference fringes in Young's double slit experiment. Suppose the mth brght fringe due to 6500Å coincides with nth bright fringe due to 5200Å at a minimum distance from the cental maximum. ThenSolution in Kannada
0.312 mm
0.123 mm
0.213 mm
0.412 mm
The correct Answer is:A
Here,
Distance between the slits , d = 2 mm =2×10−3m
Distance of the screen from the slits , D = 1.2 m
Wavelengths,
λ1=6500Å=6500×10−10=6.5×10−7m
and λ2=5200Å=5200×10−10=5.2×10−7m
Distance of nth bright fringe from the centre bright fringe is
xn=nλDd ...(i)
If x4andx4' be the distances of the fourth bright fringes of wavelengths λ1andλ2 respectively , then from eqn. (i)
x4=4λ1Ddandx'4=4λ2Dd
Thus, the separation between therm is
Δx=x'4=4λ1Dd−4λ2Dd=4D(λ1−λ2)d
=4(1.2m)(6.5×10−7m−5.2×10−7m)(2×10−3m)
=3.12×104m=0.312×10−3m=0.312mm
Topper's Solved these Questions
Similar Questions
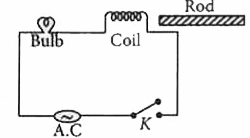
In the A. C. circuit shown, keeping 'K' pressed, if an iron rod is inserted into the coil, the bulb in the circuit
 View Solution
View SolutionWhich one of the following nuclei has shorter mean life?
 04:25View Solution
04:25View SolutionA beam of light consisting of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in YDSE. The distance between slits is 2mm and the distance of the screen form slits is 120 cm. What is the least distance from central maximum where the bright due to both wavelengths coincide?
12:06View SolutionA beam of light consisting of two wavelength 6500Å&5200Å is used to obtain interferance fringes in a young's double slit experiment .The distance between the slits is 2.0mm and the distance between the plane of the slits and thescreen is 120cm ,.what is the least distance from the central maximum where the bright fringes due to both the wave length coincides?
01:56View SolutionA beam of light consisting of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in a young's double slit experiment the distanece between the slits is 2mm and the distance between the plane of the slits and screen is 120 cm.
(a). Find the distance of the third bright fringe on the screen from the central maxima for the wavelength 6500Å
(b). What is the least distance from the central maxima where the bright fringes due to both the wave lengths coincide?03:32View SolutionA beam of light consisting of two wavelength 6300 A^(@) and lambda A^(@) is used to obtain interference frings in a Young's double slit experiment. If 4^(th) bright fringe of 6300 A^(@) coincides with 5^(th) dark fringe of lambdaA^(@) , the value of lambda (in A^(@) ) is
03:02View SolutionA beam of light consisting of two wavelength, 6500 Å and 5200 Å is used to obtain interference fringes in a Young's double slit experiment. Find the distance of the third fringe on the screen from the central maximum for the wavelength 6500Å . What is the least distance from the central maximum at whixh the bright fringes due to both wavelengths coincide? The distance between the slits is 2 mm and the distance between the plane of the slits and the screen is 120 cm.
07:08View SolutionA beam of light contains two wavelengths 6500Å and 5200Å They form interference fringes in Young's double slit experiment. What is the least distance (approx) from central maximum. Where the bright fringes due to both wavelength coincide? The distance between the slits is 2 mm and the distance of screen is 120 cm.
02:53View Solutionप्रकाश की एक बीम में मुख्यतः 6500Å तथा 5200Å तरंगदैर्घ्य के प्रकाश है । इस बीम से एक double slit को प्रकशित किया जाता है रेखाछिद्रों के बीच की दूरी 0.2 mm है तथा पर्दे एवं रेखाछिद्रों के बीच की दूरी 120 cm है (a) तरंगदैर्घ्य 6500Å के लिए पैटर्न के केंद्र से तीसरी दीप्त फ्रिंज की दूरी निकाले ।
(b) पैटर्न के केंद्र से वह न्यूनतम दूरी क्या होगी जहाँ तरंगदैर्घ्य 6500Å तथा 5200Å की दो दीप्त फ्रिंजे एक ही स्थान पर बन रही हो ?04:49View SolutionIn Young's double slit experiment slits are separated by 2 mm and the screen is placed at a distance of1.2 m from the slits. Light consisting of two wavelengths 6500Å and 5200Å are used to obtain interference fringes.
The the separation between the fourth bright fringes the two wavelength is03:49View SolutionInterference fringes are obtained in a Young's double slit experiment using beam of light consisting two wavelengths 500 nm and 600 nm. Bright fringes due to both wavelengths coincide at 2.5 mm from the central maximum. If the separation between the slits is 3 mm, then the distance between the screen and plane of the slits is
04:36View SolutionA beam of light of two wavelengths 6500Å and 5200Å, is used to obtain interference fringes in Young's double slit experiment. Suppose the mth brght fringe due to 6500Å coincides with nth bright fringe due to 5200Å at a minimum distance from the cental maximum. Then
03:08View SolutionA beam of light consisting of two wavelengths 500 nm and 400 nm is used to obtain interference fringes in Young's double slit experiment. The distance between the slits is 0.3 mm and the distance between the slits and the screen is 1.5 m. Compute the least distance of the point from the central maximum, where the bright fringes due to both the wavelengths coincide.
View SolutionIn Young's double slit experiment, if th distance between two slits is double of the wavelength of light used. Prove that maximum 5 bright fringes will be obtained on the screen.
03:16View SolutionA beam of light considering of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in a Young's double slit experiment. :) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 6500Å (ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide ? Distance a between the slits is 2 mm, distance between the slits and the screen D= 120 cm.
02:46View SolutionIn Young.s double slit experiment, slits are separated by 2 mm and the screen is placed at a distance of 1.2 m from the slits. Light consisting of two wavelengths 6500Å and 5200Å are used to obtain interference fringes. Then the separation between the fourth bright fringes of two different patterns produced by the two wavelengths is
02:56View Solution

